Consider the disk-shaft system in Problem 2 of Problem Set 5.3. The system is approximated as a single-degree-of-freedom rotational mass-spring system, where \(m=10 \mathrm{~kg}, r=0.05 \mathrm{~m}, B=1 \mathrm{~N} \cdot \mathrm{m} \cdot \mathrm{s} / \mathrm{rad}\), and \(K=1000 \mathrm{~N} \cdot \mathrm{m} / \mathrm{rad}\).

a. Assume that a torque \(\tau=50 u(t) \mathrm{N} \cdot \mathrm{m}\) is acting on the disk, which is initially at rest. Build a Simscape model of the physical system and find the angular displacement output \(\theta(t)\).

b. Assuming that the external torque is \(\tau=0\) and the initial angular displacement is \(\theta(0)=0.1 \mathrm{rad}\), find the angular displacement output \(\theta(t)\).

Data From Problem 2 of Problem Set 5.3:

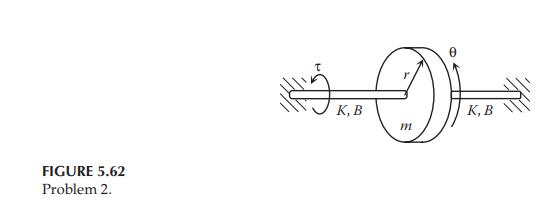
Repeat Problem 1 for the system shown in Figure 5.62.

Data From Problem 1: 

 Consider the rotational system shown in Figure 5.61. The system consists of a massless shaft and a uniform thin disk of mass m and radius r. The disk is constrained to rotate about a fixed longitudinal axis along the shaft. The shaft is equivalent to a torsional spring of stiffness K connected in parallel with a torsional viscous damper of damping coefficient B

Transcribed Image Text:

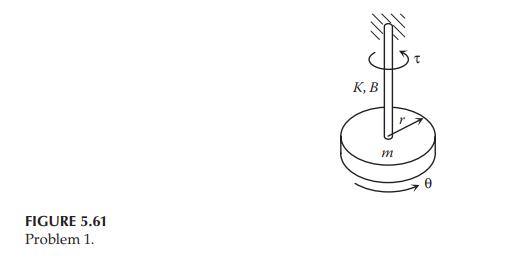
FIGURE 5.62 Problem 2. 0 K, B m K, B