Repeat Problem 3 for the two-degree-of-freedom quarter-car model in Example 5.5. Assume that the surface of the road can be approximated as a sine wave \(z=Z_{0} \sin (2 \pi v t / L)\), where \(Z_{0}=0.01 \mathrm{~m}, L=10 \mathrm{~m}\), and the speed \(v=20 \mathrm{~km} / \mathrm{h}\). If the car moves at a speed of \(100 \mathrm{~km} / \mathrm{h}\), rerun the simulations and compare the results with those obtained in the case of \(20 \mathrm{~km} / \mathrm{h}\). Ignore the control force \(f\) for both cases.

Data From Example 5.5:

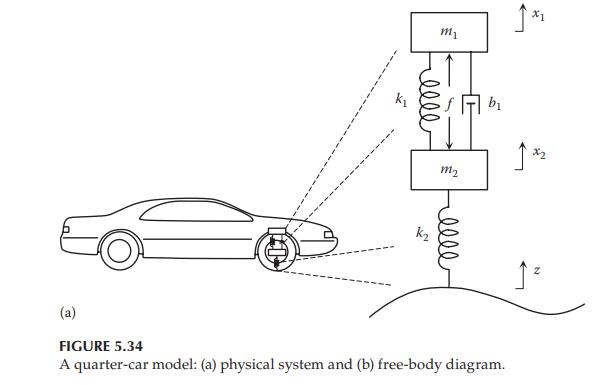
Consider a quarter-car model shown in Figure 5.34a, where m1 is the mass of one-fourth of the car body and m2 is the mass of the wheel–tire–axle assembly. The spring k1 represents the elasticity of the suspension and the spring k2 represents the elasticity of the tire. z(t) is the displacement input due to the surface of the road. The actuator force, f, applied between the car body and the wheel–tire–axle assembly, is controlled by feedback and represents the active components of the suspension system.

m k N Tu 0000 b x2 12 FIGURE 5.34 A quarter-car model: (a) physical system and (b) free-body diagram.