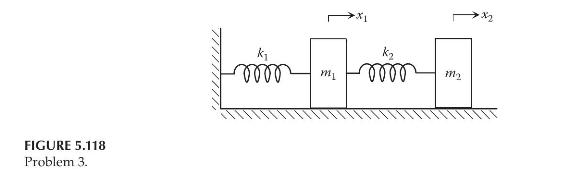
Consider the two-degree-of-freedom mass-spring system shown in Figure 5.118. The parameter values are \(m_{1}=m_{2}=5 \mathrm{~kg}, k_{1}=2000 \mathrm{~N} / \mathrm{m}\), and \(k_{2}=4000 \mathrm{~N} / \mathrm{m}\). Assume that, initially, \(\mathbf{x}(0)=\left[\begin{array}{ll}0 & 0\end{array}\right]^{T}\) and \(\dot{\mathbf{x}}(0)=\left[\begin{array}{ll}1 & 0\end{array}\right]^{T}\).

a. Build a Simulink model based on the differential equations of motion of the system and find the displacement outputs \(x_{1}(t)\) and \(x_{2}(t)\).

b. Build a Simscape model of the physical system and find the displacement outputs \(x_{1}(t)\) and \(x_{2}(t)\).

Transcribed Image Text:

FIGURE 5.118 Problem 3. k 0 0 0 0 m My