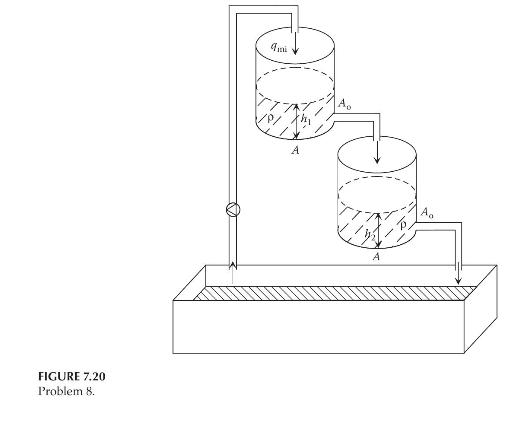
Figure 7.20 shows a hydraulic system of two interconnected tanks that have the same cross-sectional area of \(A\). A pump is connected to tank 1. Assume that the relationship between the voltage applied to the pump and the mass flow rate into tank 1 is linear; that is, \(q_{\mathrm{mi}}=k_{\mathrm{p}} v_{\mathrm{a}}\), where \(k_{\mathrm{p}}\) is called the pump constant and can be obtained by experimental measurements. Tank 1 is connected to tank 2, which is connected to a reservoir. The liquid leaves each tank through an outlet of area \(A_{\mathrm{o}}\) at the bottom. Derive the differential equations in terms of the liquid heights \(h_{1}\) and \(h_{2}\).

Transcribed Image Text:

FIGURE 7.20 Problem 8. 4mi A A