Recall from Example 10.4 that more women (29.1%) than men (11.1%) are excluded from the astronaut pilot

Question:

Recall from Example 10.4 that more women (29.1%) than men (11.1%) are excluded from the astronaut pilot program by the minimum and maximum height restrictions. What value of minimum height for women would exclude the same total proportion of women as men, given that 0.3% of women are too tall?

Data from example 10.4

NASA excludes anyone under 62 inches in height and anyone over 75 inches from being an astronaut pilot (NASA 2004). In metric units, these values for the lower and upper height restrictions are 157.5 cm and 190.5 cm, respectively. What fraction of the young adult American population is excluded from being an astronaut pilot by these height constraints? The distribution of adult heights within a gender and age group are reasonably well approximated by a normal distribution, with the mean and standard deviation for 20- to 29-year-old males in America given by 177.6 cm and 9.7 cm, respectively (McDowell et al. 2008). For 20- to 29-year-old American females, the mean height is 163.2 cm with a standard deviation of 10.1 cm.

We can use the standard normal distribution to calculate the proportion of individuals who are made ineligible for astronaut pilot training because of their height alone. We will start with the calculation for males. Let's be very specific about what we are trying to do: we want to know the probability that a 20- to 29-year-old male individual has a height that is either less than 157.5 cm or greater than 190.5 cm: Pr[Height 190.5] It becomes much easier to answer the question if we make a sketch of what we are looking for (Figure 10.4-4).

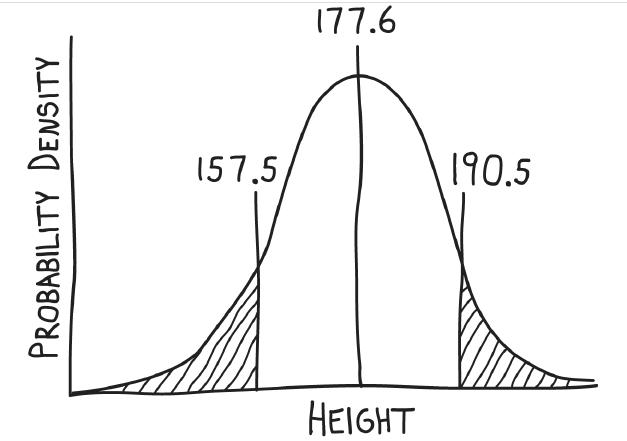
The maximum height (190.5 cm) is above the mean (177.6 cm), and the minimum height (157.5 cm) is below the mean. Based on the drawing in Figure 10.4-4, the outcomes "Height 190.5]^.Let's start with the second part first: what's the probability that an American male is too tall for NASA's restrictions? In other words, what is the probability that an American adult male is taller than 190.5 cm? The first step is to convert Height=190.5 to a standard normal deviate, using the mean (177.6 cm) and standard deviation (9.7 cm) of American male height: Z=190.5 cm-177.6 cm9.7 cm=1.33^. That is, a value of 190.5 cm occurs at 1.33 standard deviations above the mean male height. What fraction lies above this point? In other words, what is Pr[Z>1.33]?Using Statistical Table B at the end of this book, we can see that 0.09176 of the area under the standard normal distribution lies more than 1.33 standard deviations above the mean. So, this is our answer to this part of the problem: the fraction 0.09176 of American adult males are taller than 190.5 cm. Finding the probability of males being too short for NASA's restrictions follows a similar procedure, but with one additional step. Again we convert Height=157.5 (the minimum cutoff) to a standard normal deviate: Z=157.5 cm-177.6 cm9.7 cm=-2.07.In other words, 157.5 cm occurs at 2.07 standard deviations below the mean male height. What fraction of American adult males lies below this point? What is Pr[Z Statistical Table B gives us the probability of obtaining a value greater than a given number. To find the probability of getting a value less than a particular number, remember that the normal distribution is symmetric around its mean. Thus, the probability of being 2.07 standard deviations or more below the mean is the same as the probability of being 2.07 standard deviations or more above the mean: Pr[Z 2.07] When we look up the probability of being greater than 2.07 in Statistical Table B, we find that Pr[Z>2.07] =0.01923. Thus, the fraction 0.01923 of American adult males are shorter than 157.5 cm. Now, use the addition rule to determine the proportion of American adult men that are excluded from the astronaut pilot program by the height restrictions: Pr[Height 190.5] =0.01923+0.09176 = 0.11099. The fraction 0.11099 (or 11.1%) of all 20- to 29-year-old American adult males are excluded by height. In other words, the NASA height restriction excludes a modest percentage of men. We can make similar calculations for American adult women. Women’s heights are approximated by a normal distribution with mean 163.2 cm and standard deviation 10.1 cm. These values correspond to height restrictions at 0.56 standard deviations below the mean and 2.7 standard deviations above the mean. (Check these numbers for yourself.) Using Statistical Table B, the fraction 0.28774 of the women are too short to meet NASA’s guidelines and the fraction 0.00347 are too tall. In total, the height restrictions exclude 29.1% of young American women from being astronaut pilots.