Let’s test this out for the infinite square well, where we will set the width a = 1 of the well for simplicity. That is, the potential we consider is

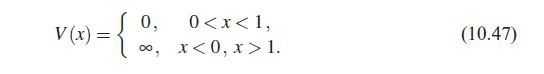
We know what the ground-state energy is in this case

where I have expanded the numerical value of π2/2 to seven significant figures. Now, on to a guess for the ground-state wavefunction. We know that the wavefunction must vanish at both x = 0,1, the boundaries of the well. Additionally, the well is symmetric about its central point x = 1/2, so we expect that the wavefunction would also be symmetric about x = 1/2. A guess for a wavefunction that vanishes at the endpoints and is symmetric about x = 1/2 is

where N is a normalization constant and α is a parameter we will vary to minimize the expectation value of the Hamiltonian on this state.

Transcribed Image Text:

0, v(x) = { 0%. 009 0 1. (10.47)