27. Let X1, . . . ,Xn be independent random variables with E[Xi] = , Var(Xi) =...

27. Let X1, . . . ,Xn be independent random variables with E[Xi] = θ, Var(Xi) = σ2 i

i = 1, . . . , n, and consider estimates of θ of the form

ni

=1 λiXi where

ni

=1 λi = 1.

Show that Var

ni

=1 λiXi

is minimized when

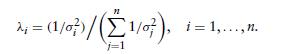
Possible Hint: If you cannot do this for general n, try it first when n = 2.
The following two problems are concerned with the estimation of 1 0 g(x) dx = E[g(U)]
where U is uniform (0, 1).

Transcribed Image Text:

= (1/0)/([1/07), i = 1,..., n.