36. Let S(t) denote the price of a security at time t. A popular model for the process

{S(t), t 0} supposes that the price remains unchanged until a “shock” occurs, at which time the price is multiplied by a random factor. If we let N(t) denote the number of shocks by time t, and let Xi denote the ith multiplicative factor, then this model supposes that

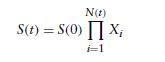
where 2N(t)
i=1 Xi is equal to 1 when N(t) = 0. Suppose that the Xi are independent exponential random variables with rate μ; that {N(t), t 0} is a Poisson process with rate λ; that {N(t), t 0} is independent of the Xi ; and that S(0) = s.

(a) Find E[S(t)].

(b) Find E[S2(t)].

Transcribed Image Text:

N(t) S(t) = S(0) Xi i=1