Use the results of Example 13.5 (Section 13.3) to calculate the escape speed for a spacecraft

(a) From the surface of Mars and

(b) From the surface of Jupiter. Use the data in Appendix F.

(c) Why is the escape speed for a spacecraft independent of the spacecraft's mass?

In Example 13.5:

In Jules Verne's 1865 story with this title, three men went to the moon in a shell fired from a giant cannon sunk in the earth in Florida. (a) Find the minimum muzzle speed needed to shoot a shell straight up to a height above the earth equal to the earth's radius R_E. (b) Find the minimum muzzle speed that would allow a shell to escape from the earth completely (the escape speed). Neglect air resistance, the earth's rotation, and the gravitational pull of the moon. The earth's radius and mass are R_E = 6.38 × 10⁶ m and m_E = 5.97 × 10²⁴ kg.

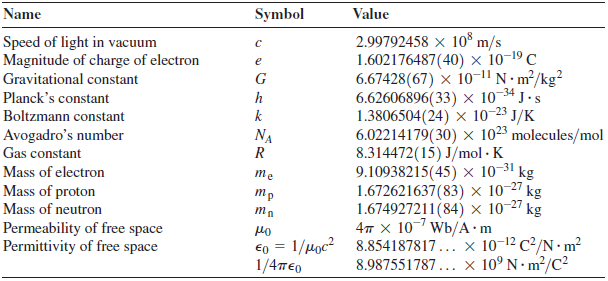
Appendix F:

Fundamental Physical Constants*

Transcribed Image Text:

Name Symbol Value 2.99792458 x 10® m/s 1.602176487(40) × 10-1º c 6.67428(67) × 10-1! N •m²/kg² 6.62606896(33) × 10-34 J .s 1.3806504(24) × 10–23 J/K 6.02214179(30) × 1023 molecules/mol 8.314472(15) J/mol · K 9.10938215(45) × 10-31 kg 1.672621637(83) × 10-27 kg 1.674927211(84) × 10-27 kg 4m x 10-7 Wb/A•m 8.854187817... × 10-12 C²/N• m? 8.987551787... × 10º N • m²/C² Speed of light in vacuum Magnitude of charge of electron Gravitational constant G Planck's constant Boltzmann constant k NA Avogadro's number Gas constant Mass of electron me Mass of proton Mass of neutron Permeability of free space Permittivity of free space 1/Học2 1/4πεο