Suppose that two people are engaged in a Vickrey auction for a good with two possible values: $10 or $20. Further, suppose each bidder receives a signal of the value, x_n, where x_n is equal to the true value with probability 0.8, and equal to the other possible value with probability 0.2. No information other than this signal is available. Each player must select a bid based on his own signal. What bidding strategy would be suggested by the fully cursed equilibrium (e.g., what should you bid if you receive a signal of $10 and what should you bid if you receive a signal of $20)? Suppose that players can only bid integer amounts, and follow the example given in the text. Thus, if player 1 draws x₁ = 10, the mean value of winning the auction is

,

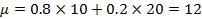The probability of signals that player 2 might receive is (similar to equation 5.13)

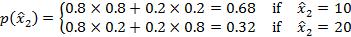
If player 1 draws x₁ = 20, the expected value of winning the auction is μ = 0.8 x 20 + 0.2 x 10 = 18, and the probability distribution of signals that player 2 might receive is

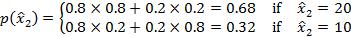
Suppose that in the event of a tie, both players receive the value of the object. First try the strategy in which each player bids the expected value of the gamble given the signal each has received. Show that this constitutes a cursed equilibrium. What is the expected profit in this case (the actual, not perceived)? Do these strategies constitute a Bayesian Nash equilibrium? If not, can you find the Bayesian Nash equilibrium?

Transcribed Image Text:

X-1スX0:: 置。::10