Suppose the current density changes slowly enough that we can (to good approximation) ignore all higher derivatives
Question:
Suppose the current density changes slowly enough that we can (to good approximation) ignore all higher derivatives in the Taylor expansion J(tr) = J(t) + (tr ?? t) J (t) +... (for clarity, I suppress the r-dependence, which is not at issue). Show that a fortuitous cancellation in Eq. 10.31 yields That is: the Biot-Savart law holds, with J evaluated at the non-retarded time. This means that the quasistatic approximation is actually much better than we had any right to expect: the two errors involved (neglecting retardation and dropping the second term in Eq. 10.31) cancel one another, to first order.
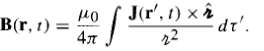
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





