The ideal Hilbert transformer (90-degree phase shifter) has frequency response (over one period) Figure shows H(e^j?), and Figure shows the frequency response of an ideal lowpass filter H_IP(e^j?) with cutoff frequency ?_C = ?/2. These frequency responses are clearly similar, each having discontinuities separated by ?.

(a) Obtain a relationship that expresses H(e^j?) in terms of H_IP(e^j?). Solve this equation for H_IP(e^j?) in terms of H(e^j?).

(b) Use the relationships in part (a) to obtain expressions for h[n] in terms of h_IP[n] and for h_IP[n] in terms of h[n].

The relationships obtained in parts (a) and (b) were based on definitions of ideal systemswith zero phase. However, similar relationships hold for nonidea, systems with generalized linear phase.

(c) Use the results of Part (b) to obrain a relationship between the impulse response of a causal FIR approcimation to the Hilbert transformer and the impulse response of a causal FIR approximation to the lowpass filter, both of which arer designed by (1) incorporating an appropriate linear phase, (2) determining the corresponding ideal impulse response, and (3) multiplying by the same window of length (M + 1) samples, i.e., by the window method discussed in Chapter 7. (If necessary, sonsider the cases of M even and M odd separately.)

(d) For the Hilbert transformer approximations of Example 11.4, sketch the magnitude of the frequency responses of the corresponding lowpass filters.

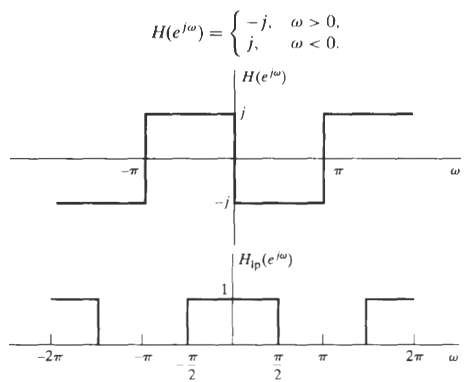
-j. w > 0, j. H(el") = H(e) H,(e ) -2