In Section 11.4.3, we discussed an efficient scheme for sampling a bandpass continuous-time signal with Fourier transform such that?

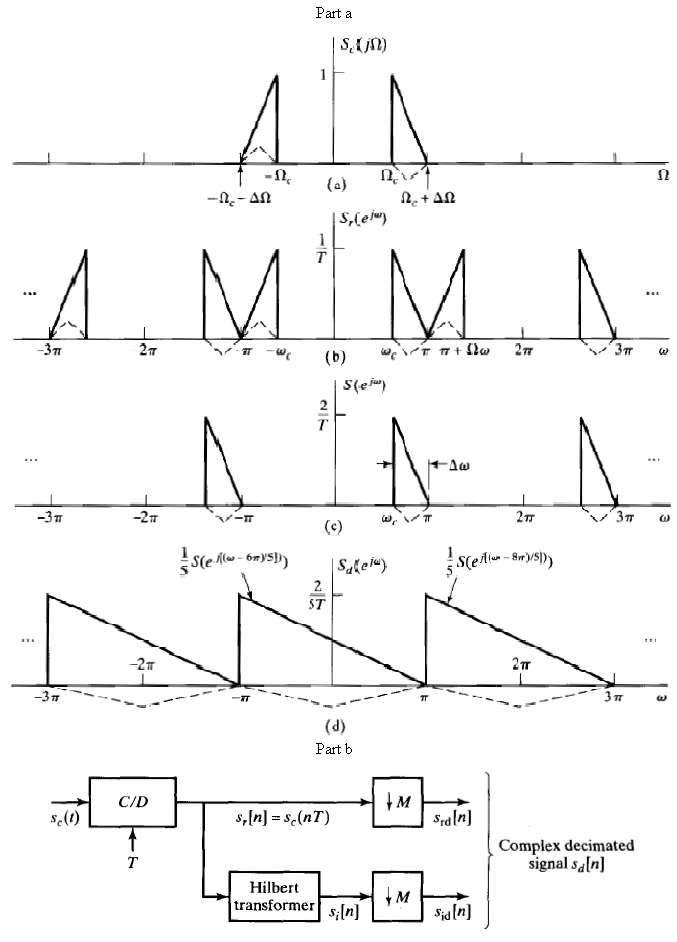
S_c(j?) = 0? ? ? ??for |?| ? ?_c and |?| ? ?_c + ??.

In that discussion, it was assumed that the signal was intially sampled with sampling frequency 2?/T = 2(?_c + ??), i.e., at the lowest possible frequency that aviods aliasing. The bandpass sampling scheme is depicted in Figure. After we form a complex bandpass discrete-time dignal s[n] with one-sided Fourier transform S(e^j?), the complex signal is decimated by a factor M, which is assumed to be the largest integer less than or equal to 2?/(??T).

(a) By carrying through an example such as the one depicted in Figure, show that if the quantity 2?/(??T) is not an integer for the initial sampling rate chosen, then the resulting decimated signal s_d[n] will have regions of nonzero length where its Fourier transform S_d(e^j?) is identically zero.

(b) How should the initial sampling frequency 2?/T be chosen so that a decimation factor M can be found such that the decimated sequence s_d[n] in the system of Figure will have a Fourier transform S_d(e^j?) that is not alilased, yet has non regions where it is zero over an interval of nonzero length? ?

Part a | S,AN) 12 (a) -n.-AN |S,(eju) A,MIM.A -37 27 (b) S(ea) -27 -37 (c) s(e K- onyS)) S(eAl - Bim)/S) | Salele) ST -2m 2 -37 (d) Part b +M Sraln] C/D s,[n] = s,(nT) se(t) Complex decimated signal saln] Hilbert transformer s;[n] Sidln]