With reference to Definition 4.4, show that 0 = 1 and that 1 = 0

Question:

With reference to Definition 4.4, show that µ₀ = 1 and that µ₁ = 0 for any random variable for which E(X) exists.

Definition 4.4

The rth moment about the mean of a random variable X, denoted by µ_r, is the expected value of ( X – µ)^r, symbolically

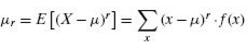
For r = 0, 1, 2, . . . , when X is discrete, and

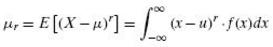
When X is continuous.

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For book-img-for-question

John E Freunds Mathematical Statistics With Applications

ISBN: 9780134995373

8th Edition

Authors: Irwin Miller, Marylees Miller

See More Books

Question Posted: Nov 04, 2015 03:05 AM

See More Questions

Show that if 1 < 0 in Example 12.4, the Neyman-Pearson lemma yields the critical region IS po - Za
With reference to the generalized definition of binomial coefficients in Exercise 1.19, show that (a) (b) -l r) = (1)r (n+r-1 for n>0
With reference to Exercise 5.12, find the factorial momentgenerating function of (a) The Bernoulli distribution and show that µ'(1) = . and µ'(r) = 0 for r > 1; (b) The binomial...
A manufacturer of packaging for companies that produce breakfast cereals is considering alternatives regarding the process it uses to pre-process carton paper used to make the packaging....
Use Table 2 in Appendix B to determine the critical region used in testing each of the following hypotheses. a. Ho: p = 0.5 and Ha: p > 0.5 where n = 15 and a = 0.05 b. Ho: p = 0.5 and Ha: p 0.3...
Co.s purchases and sales of a particular product during the year are shown below: Jan. 1 Beginning Inventory 1,500 units @ $ 10 Jan. 18 Purchase 1,250 units @ $ 12 Jan 20 Sold 1,500 units @ $ 20 Jan....
such as facilities and equipment?
Sara Collier, the bookkeeper for Danner, Cheney, and Howe, a political consulting firm, has recently completed an accounting course at her local college. One of the topics covered in the course was...
nonprogress-Tase 18 Entries for issuing and Calling Bonds; Gain Emil Corp. produces and sells wind-energy-driven engines. To finance its operations, Emil Corp, issued $621,000 of 25 year 14% callable...
Personal automobile policy coverage. Brando poli Dougherty has a personal automobile on (PAP) with coverage of $25,000/$50,000 for b ily injury liability, $25,000 for property damage liability,...
If the probability distribution of X is given by f(x) = (1/2)x for x = 1, 2, 3, . . . show that E(2X) does not exist. This is the famous Petersburg paradox, according to which a players expectation...
Find , '2, and s2 for the random variable X that has the probability distribution f(x) = 12 for x = 2 and x = 2.
Based on your own leadership style, would you make a good coach? Why or why not?
The following data apply to Superior Auto Supply Inc. for May 2011. 1. Balance per the bank on May $31, \$ 8,000$. 2. Deposits in transit not recorded by the bank, $\$ 975$. 3. Bank error; check...
How do you determine whether there is a linear correlation between two variables $x$ and $y$ ? Use Table 14.10. Table 14. 10 n a = 0.05 0.950 0.878 4 5 6 0.811 7 0.754 8 0.707 9 0.666 10 0.632 11...
Comparative Analysis Problem: Columbia Sportswear Company vs. Under Armour, Inc. The financial statements for the Columbia Sportswear Company can be found in Appendix A and Under Armour, Inc.'s...
The following information is available for Book Barn Company's sales on account and accounts receivable: After several collection attempts, Book Barn wrote off $\$ 4,500$ of accounts that could not...
The following information comes from the accounts of Jersey Company: Required a. There were $\$ 170,000$ of sales on account during the accounting period. Write-offs of uncollectible accounts were...
There are thought to be three types of the particles called neutrinos: electrontype $\left(u_{e} ight)$, muon type $\left(u_{\mu} ight)$, and tau-type $\left(u_{\tau} ight)$. If they were all...
You are standing on the top of a building and throw a ball vertically upward. After 2 seconds, the ball passes you on the way down, and 2 seconds after that, it hits the ground below. a. What is the...
EX 10.3 Draw and annotate a class hierarchy that represents various types of sales transactions in a store (cash, credit, etc.). Show what characteristics would be represented in the various classes...
The Georgetown, South Carolina, Traffic Division reported 40% of high-speed chases involving automobiles result in a minor or major accident. During a month in which 50 high-speed chases occur, what...
Cruise ships of the Royal Viking line report that 80% of their rooms are occupied during September. For a cruise ship having 800 rooms, what is the probability that 665 or more are occupied in...
The goal at U.S. airports handling international flights is to clear these flights within 45 minutes. Lets interpret this to mean that 95% of the flights are cleared in 45 minutes, so 5% of the...
Ellis Perry is an electronics components manufacturer. Information about the company's two products follows: \ table [ [ , , , ] , [ Units produced,AM - 2 , FM - 9 , ] , [ Direct labor hours required...
Which of the following requirements to claim Earned Income Tax Credit is TRUE? The credit can be claimed under any filing status. The taxpayer must have a valid SSN for employment in the U.S., issued...
Olde Tyme Beverage Companys operating activities for the year are listed below. Cost of Goods Manufactured $131,000 Operating expenses 80,000 Beginning inventory, FG 16,000 Ending inventory, FG...

With reference to Definition 4.4, show that 0 = 1 and that 1 = 0

Question:

4, = E[(X-uY] = Ea-u f)

Step by Step Answer:

H fx fx d...View the full answer

John E Freunds Mathematical Statistics With Applications

Students also viewed these Statistics questions