With the notation used in this chapter 

(a) What is N'(x)?

(b) Show that SN'(d₁) = Ke^–r(T–t)N'(d₂), where S is the stock price at time t 

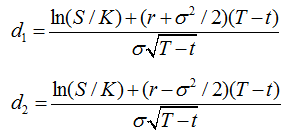
(c) Calculate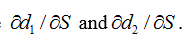  

(d) Show that when

where c is the price of a call option on a non-dividend-paying stock. 

(e) Show that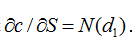 

(f) Show that the c satisfies the Black–Scholes–Merton differential equation. 

(g) Show that  satisfies the boundary condition for a European call option, i.e., that c = max (S –k, 0) as t tends to T. 

Transcribed Image Text:

In(S /K)+(r+o² / 2)(T – t) d ONT -t In(S /K)+(r-o² / 2)(T – t) dz oNT -t ôd, / ôS and od, / OS .