Consider, sampling from a multivariate normal distribution with mean vector = (1, 2, . . .
Question:
Consider, sampling from a multivariate normal distribution with mean vector μ = (μ1, μ2, . . . , μM) and covariance matrix σ2I. The log-likelihood function is Show that the maximum likelihood estimates of the parameters are Derive the second derivatives matrix and show that the asymptotic covariance matrix for the maximum likelihood estimators is Suppose that we wished to test the hypothesis that the means of the Mdistributions were all equal to a particular value μ0. Show that the Wald statistic would be where ?y is the vector of sample means.br>
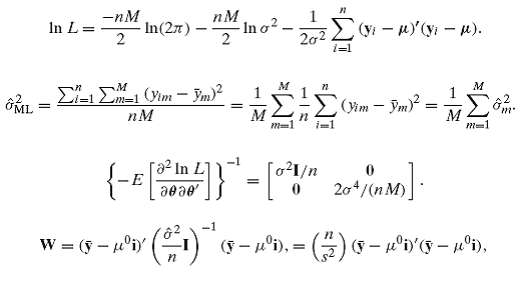
The word "distribution" has several meanings in the financial world, most of them pertaining to the payment of assets from a fund, account, or individual security to an investor or beneficiary. Retirement account distributions are among the most...
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





