Soft phonon mode consider a line of ions of equal mass but alternating in charge, with e
Question:
Soft phonon mode consider a line of ions of equal mass but alternating in charge, with ep = e(?1)p as the charge on the pth ion the inter atomic potential is the sum of two contributions (1) a short-range interaction of force constant C1R = ? that acts between nearest neighbors only, and (2) a coulomb interaction between all ions.?
(a) Show that the contribution of the coulomb interaction to the atomic force constants is CpC?= 2(?1)p e2/p3?a3, where a is the equilibrium nearest-neighbor distance.?
(b) From (16a) show that the dispersion relation may be written as where w20 ? 4?/M and ? = e2/?a3.
(c) Show that w2 is negative (unstable mode) at the zone boundary Ka = ? if ? > 0.475 or 4/7? (3), where ? is a Riemann zeta function. Show further that the speed of sound at small Ka is imaginary if ? > (2 In 2)?1?= 0.721. Thus w2 goes to zero and the lattice is unstable for some value of Ka in the interval (0, ?) if 0,475
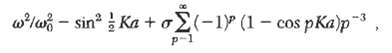
Step by Step Answer:






