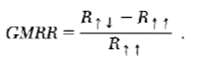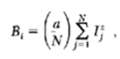Introduction to Solid State Physics 8th Edition Charles Kittel - Solutions
If you're seeking comprehensive guidance on "Introduction to Solid State Physics 8th Edition" by Charles Kittel, you're in the right place. Our platform offers a complete range of solutions, including a solution manual and answers key. Dive into step-by-step answers to all chapter solutions, ensuring you grasp each concept with ease. Access solved problems and an extensive test bank to bolster your understanding. Whether you're looking for the instructor manual or solutions PDF, our resources are tailored for effective learning. Enhance your study experience with our free download of these invaluable textbook resources.
![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


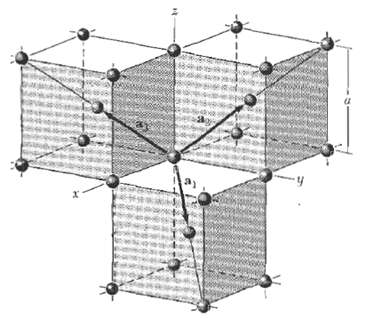
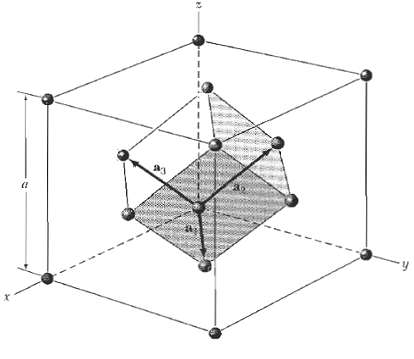
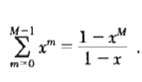
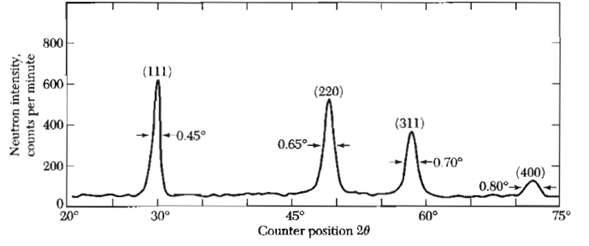
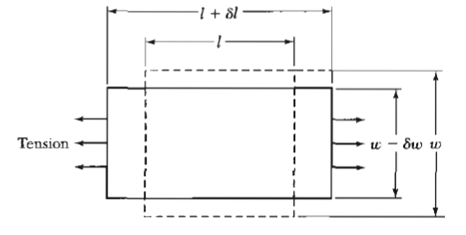
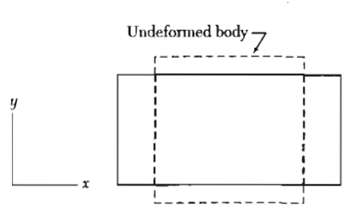
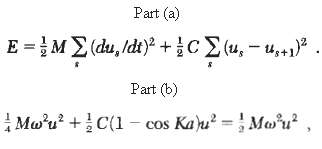
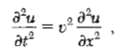
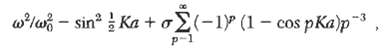
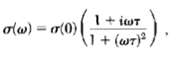
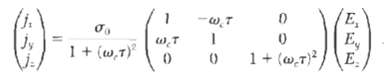
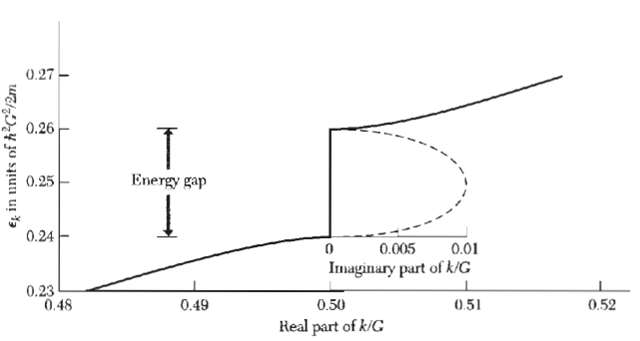
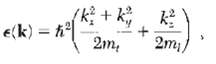
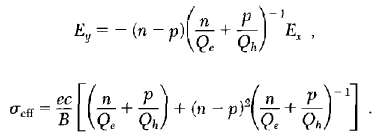
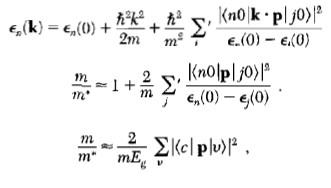
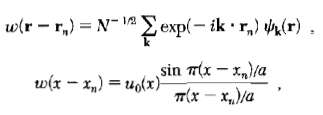
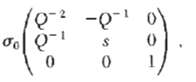
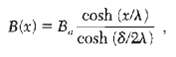
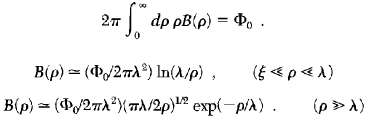
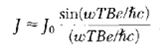
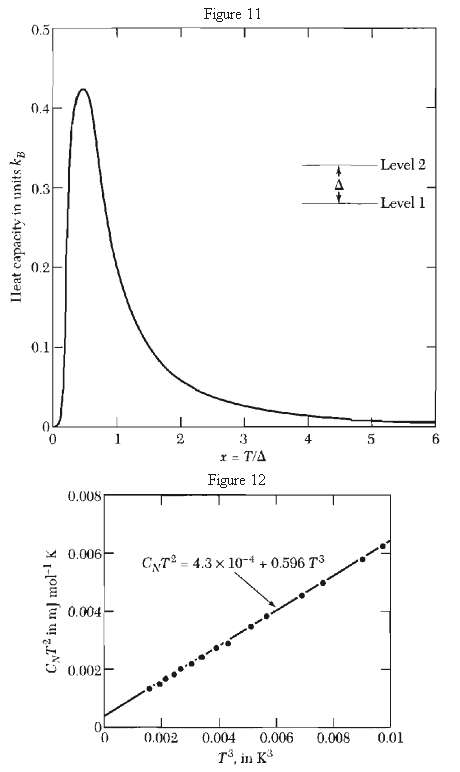
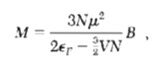
![ds;jdt = (2]S/k)(6S% – S.) .](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1548/7/6/3/1745c5040269f4be1548763174134.jpg)