(a) Show that I = « C (x 2 y dx + 2xy 2 dy) is path dependent in the xy-plane. (b) Integrate from (0,

(a) Show that I = ˆ«_C (x²y dx + 2xy²dy) is path dependent in the xy-plane.

(b) Integrate from (0, 0) along the straight-line segment to (1, b), 0 ‰¤ b ‰¤ 1, and then vertically up to (1, 1); see the figure. For which b is I maximum? What is its maximum value?

(c) Integrate I from (0, 0) along the straight-line segment to (c, 1), 0 ‰¤ c ‰¤ 1, and then horizontally to (1, 1). For c = 1, do you get the same value as for b = 1 in (b)? For which c is I maximum? What is its maximum value?

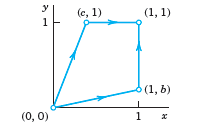
(c, 1) (1, 1) 6(1, 6) (0, 0)