The classical RK for a first-order ODE extends to second-order ODEs. If the ODE is y" = f(x, y), not containing y', then

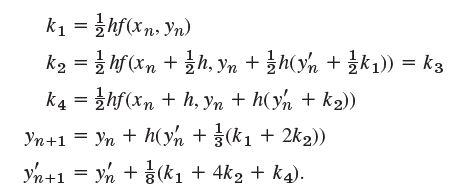
Apply this RKN (Runge€“Kutta€“Nyström) method to the Airy ODE in Example 2 with h = 0.2 as before, to obtain approximate values of Ai(x).

Transcribed Image Text:

k1 = }hf(xn, Yn) k2 = 3 hf (xn + }h, yn + h(yn + 3k1)) = k3 k4 = zhf(Xn + h, Yn + h( yn + k2)) %3D Yn+1 = yn + h(yn + (k1 + 2k2)) yn +1 = yn + (k1 + 4k2 + k4).