Consider Problem 16.22, but for the case when the unconverted reactants are recycled to the reactor, as
Question:
Consider Problem 16.22, but for the case when the unconverted reactants are recycled to the reactor, as shown in Figure P16.23. Consider the purge-stream flow to be 2% of the total flow of Stream 6, and assume that compressor C-1001 has an isentropic efficiency of 80%. Maximize the following objective function: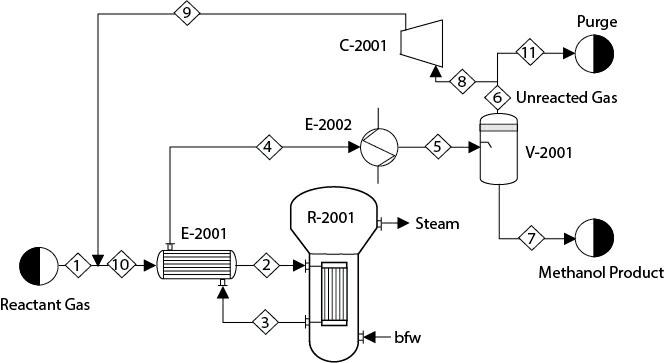
![]()
where![]()
and![]()
is the hourly flowrate of methanol in Stream 7. CUC = $0.15/kWh is the cost of electricity, and PUC is the hourly power consumption in C-2001.
The decision variables are inlet temperature and pressure of Stream 1, dimensions of R-2001, and CO/H2 ratio in Stream 1. Solve this optimization problem with the SM and EO approaches and compare the optimal values of the decision variables with the values that you obtained in Problems 16.21 and 16.22. Did you have to consider any additional constraints for this optimization problem? Why?
Problems 16.22
In the preceding problem, the composition of the feed was assumed to be constant. However, the CO/H2 ratio in the feed can be manipulated as these streams are usually supplied from different sources. Solve the preceding optimization problem by considering the CO/H2 ratio as another decision variable. Did you have to consider any additional constraints? Why? Compare the results with the results that you obtained in Problem 16.21.
Problem 16.21
In a process for producing methanol, synthesis gas composed of CO, CO1, H1, and H2O is sent through a heat exchanger, E- 2001, to a plug-flow reactor, R-2001, as shown in Figure P16.21. In addition to the desired methanol synthesis, some undesired reactions also take place: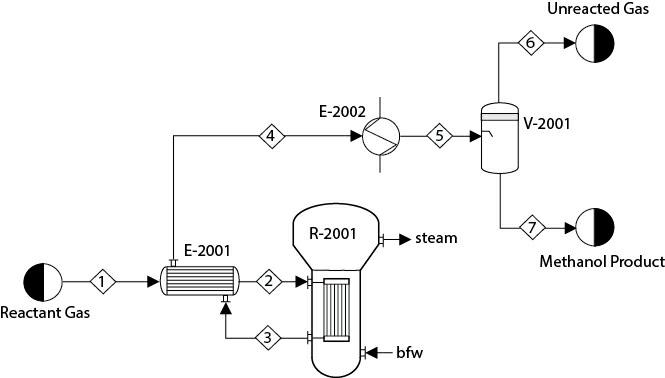
![The corresponding rate laws for these reactions are [22, 23] TCH, OH -TCO kmol kmol kg cat s CO + 2H CH3 OH](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1699/3/5/4/419654a1733733ae1699354413651.jpg)
where C is the concentration of the species i in kmol/m3.
In R-2001, steam is being generated at a temperature of 350°C. Consider an overall heat transfer coefficient of 80 W/m °C between the process stream and the boiling water. The reactor effluent is sent to E-2001 and then further cooled in E-2002 to 40°C before being sent to the flash separator, V-2001. Unconverted reactants are recovered from the top of V-2001. Assume that the feed composition (mole fraction) and rate are
The minimum temperature approach in E-2001 is 15°C. Further assume that the pressure drops in both the shell and tube sides of E-2001 are 0.1 bar. The catalyst particle density is 1800 kg/m and the bed voidage is 0.45. Assume the pressure drop in R- 2001 is 0.2 bar. Maximize the yield of methanol in this process, where the decision variables are the inlet temperature, the pressure of Stream 1, and the dimensions of R-2001 (length and diameter). What bounds on the decision variables did you consider? Why? You can solve this problem with either the SM or EO approach.
Step by Step Answer:

Analysis Synthesis And Design Of Chemical Processes
ISBN: 9780134177403
5th Edition
Authors: Richard Turton, Joseph Shaeiwitz, Debangsu Bhattacharyya, Wallace Whiting





