Consider the inspection described in Example 2.11. Six parts are selected randomly without replacement from a bin
Question:
Consider the inspection described in Example 2.11. Six parts are selected randomly without replacement from a bin of 50 parts. The bin contains 3 defective parts and 47 nondefective parts. Let \(A\) and \(B\) denote the events that the first and second parts are defective, respectively.
Example 2.11
A bin of 50 manufactured parts contains 3 defective parts and 47 nondefective parts. A sample of 6 parts is selected without replacement. That is, each part can be selected only once, and the sample is a subset of the 50 parts. How many different samples are there of size 6 that contain exactly 2 defective parts?
A subset containing exactly 2 defective parts can be formed by first choosing the 2 defective parts from the 3 defective parts. Using Equation 2.4, the number of different ways this step can be completed is
\[ \left(\begin{array}{l} 3 \\ 2 \end{array}\right)=\frac{3 !}{2 ! 1 !}=3 \]
Equation 2.4
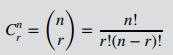
Step by Step Answer:

Applied Statistics And Probability For Engineers
ISBN: 192504
7th Edition
Authors: Montgomery, Douglas C., Runger, George C.





