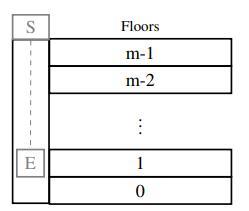
Assume the elevator of the Disney Tower of Terror E follows a Markovian process and has m floors at which it can stop. In the dead of night, you install a sensor S at the top of the shaft that gives approximate distance measurements, quantized into n different distance bins. Assume that the elevator stops at T floors as part of the ride and the initial distribution of the elevator is uniform over the m floors as shown in Figure S14.4.

You want to know the most probable sequence of (hidden) states X_1:T given your observations y_1:T from the sensor, so you turn to the Viterbi algorithm, which performs the following update at each step:

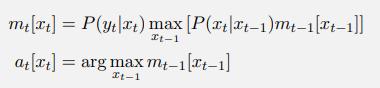
a. What is the runtime and space complexity of the Viterbi algorithm to determine all previous states for this scenario? 

b. If we only want to determine the previous K states, what is the runtime and space complexity of the Viterbi algorithm to determine the previous K states? 

c. Suppose you instead only wish to determine the current distribution (at time T) for the elevator, given your T observations, so you use the forward algorithm, with update step shown here:

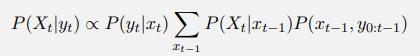
Additionally, from your previous analysis, you note that there are some states which are unreachable from others (e.g., the elevator cannot travel from the top floor to the bottom in a single timestep). Specifically, from each state, there are between G/2 and G states which can be reached in the next timestep, where G < m. What is the runtime and space complexity for the forward algorithm to estimate the current state at time T, assuming we ignore states that cannot be reached in each update? 

d. Suppose you decide to use a particle filter instead of the forward algorithm. What is the runtime of a particle filter with P particles?

Figure S14.4

Transcribed Image Text:

mt[xt] = P(yt|xt) max [P(xt|xt-1)mt-1[xt-1]] It-1 at [x] = arg max mt-1 [xt-1] It-1