Pacman finds himself inside the grid world MDP depicted in Figure S17.5. Each rectangle represents a possible state. At each state, Pacman can take actions up, down, left or right. If an action moves him into a wall, he will stay in the same state. At states A and B, Pacman can take the exit action to receive the indicated reward and enter the terminal state, E. Note R(s, a, s') = 0 otherwise. Once in the terminal state the game is over and no actions can be taken. Let the discount factor γ = 1/2 for this problem, unless otherwise specified. 

a. (i) What is the optimal action at state S? 

(ii) How many iterations k will it take before V_k(S) = V^∗ (S)? 

(iii) What are all the values that V_k(S) will take on during the entire process of value iteration. 

b.Now Ghost wants to mess with Pacman. She wants to change some of the rules of this grid world so that Pacman does not exit from state A. All subquestions are independent of each other so consider each change on its own. 

(i) First, Ghost wants to change the discount factor. Write a bound on the discount factor that guarantees Pacman exits from B instead of A. Any valid value of γ ∈ (0, 1] that satisfies your inequality should cause Pacman to exit from B instead of A. 

(ii) Next, Ghost thinks she can change the reward function to accomplish this. Write a bound on the reward from A, R(A, exit, E), that guarantees Pacman exits from B instead of A? Any value of R(A, exit, E) that satisfies your inequality should cause Pacman to exit from B instead of A. 

(iii) Ghost came up with a bunch of reward functions, R' (s, a, s'). Select the new reward functions that cause Pacman not to exit from state A. Note R(s, a, s') is the original reward function from the problem description so the reward from every state is going to be affected. 

(A) R' (s, a, s') = 1 + R(s, a, s') 

(B) R' (s, a, s') = 100 + R(s, a, s') 

(C) R' (s, a, s') = −1 + R(s, a, s') 

(D) R' (s, a, s') = −100 + R(s, a, s') 

(E) R' (s, a, s') = −R(s, a, s')

(F) R' (s, a, s') = 2R(s, a, s') 

(iv) Ghost realizes she can stop Pacman from exiting from A by adding a certain amount of grids, x, in between C and A as depicted in Figure S17.6. Give a lower bound for x that guarantees Pacman does not exit from A.

c. Another way that Ghost can mess with Pacman is by choosing parameters such that Pacman’s value iteration never converges. Select which reward function and discount factor pairs cause value iteration to never converge. 

(A) R'(s, a, s') = 100 + R(s, a, s') , γ = 0.9 

(B) R^' (s, a, s') = −100 + R(s, a, s') , γ = 0.9 

(C) R' (s, a, s') = −1 + R(s, a, s') , γ = 1.0 

(D) R' (s, a, s') = 1 + R(s, a, s'), γ = 1.0

Figure S17.5

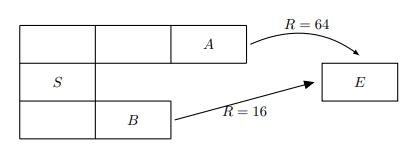
S B A R = 16 R = 64 E