The Nave Bayes model has been famously used for classifying spam. We will use it in the bag-of-words model: Each email has binary label

The Na¨ıve Bayes model has been famously used for classifying spam. We will use it in the “bag-of-words” model: 

• Each email has binary label Y which takes values in {spam, ham}. 

• Each word w of an email, no matter where in the email it occurs, is assumed to have probability P(W = w | Y ), where W takes on words in a pre-determined dictionary. Punctuation is ignored. 

• Take an email with K words w₁, . . . , w_K. For instance: email “hi hi you” has w₁ = hi, w₂ = hi, w₃ = you. Its label is given by:

a. You are in possession of a bag of words spam classifier trained on a large corpus of emails. Below is a table of some estimated word probabilities.

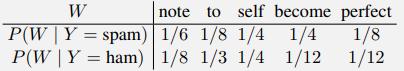
You are given a new email to classify, with only two words:

perfect note

For what threshold value, c, in the expression P(Y = spam) > c, will the bag of words model predict the label “spam” as the most likely label?

b. You are given only three emails as a training set:

(Spam) dear sir, I write to you in hope of recovering my gold watch.

(Ham) hey, lunch at 12?

(Ham) fine, watch it tomorrow night. 

Given the training set, what are the probability estimates for: 

(i) P(W = sir | Y = spam) 

(ii) P(W = watch | Y = ham) 

(iii) P(W = gauntlet | Y = ham) 

(iv) P(Y = ham) 

c. Becoming less na¨ıve

We are now going to improve the representational capacity of the model. Presence of word wi will be modeled not by P(W = w_i | Y), where it is only dependent on the label, but by P(W = w_i | Y, W_i−1), where it is also dependent on the previous word. The corresponding model for an email of only four words is given on the right.

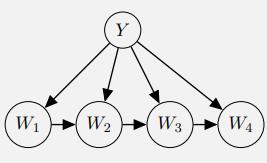 (i) With a vocabulary consisting of V words, what is the minimal number of conditional word probabilities that need to be estimated for this model?

(ii) Which of the following are expected effects of using the new model instead of the old one, if both are trained with a very large set of emails (equal number of spam and ham examples)?

A. The entropy of the posterior P(Y |W) should on average be lower with the new model. (In other words, the model will tend to be more confident in its answers.)

B. The accuracy on the training data should be higher with the new model.

C. The accuracy on the held-out data should be higher with the new model.

arg max P(Y = y | w,..., wK): = arg max P(Y = y) II/ P(W = w; | Y = y). y y