In Example 2, interchange the denominators of 4 and 16; find the vertices, ends of the conjugate axis, and foci. Sketch the curve.

Data from Example 2

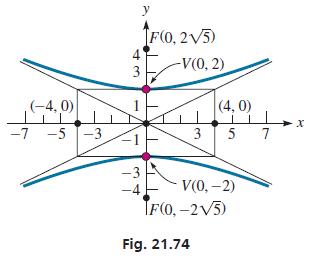
The hyperbola

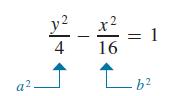
has vertices at (0,−2) and (0, 2). Its conjugate axis extends from (−4, 0) to (4, 0). The foci are (0,−2 5) and (0, 2 5). We find this directly from the equation because the y² -term is the positive term with 1 on the right. This means the equation fits the form of Eq. (21.24) with a² = 4 and b² = 16. Also, c² = 20, which means that c = √20 = 2√5.

Because 2a extends along the y-axis, we see that the equations of the asymptotes are y = ±(a/b)x. This is not a contradiction of Eq. (21.23) but the extension of it for a hyperbola with its transverse axis along the y-axis. The ratio a/b gives the slope of the asymptote. The hyperbola is shown in Fig. 21.74.

a y 4 16 = 1 || b