Define and show (by setting z = xy and then substituting z for y) that Deduce that
Question:
Define
![J = ] = exp(-1/z) dz](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1700/9/2/3/634656208f23d0111700923628090.jpg)
and show (by setting z = xy and then substituting z for y) that
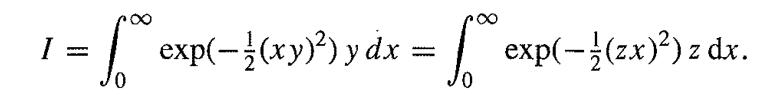
Deduce that
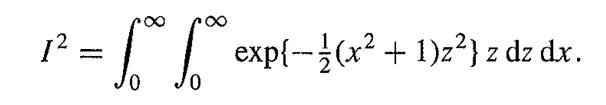
By substituting (I + x2)z2 = 2t, so that z dz = dt /(1 + x2) show that I = √π/2, so that the density of the standard normal distribution as defined in Section 1.3 does integrate to unity and so is indeed a density.
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





