Given the implicit function

find the explicit functions

(a) y = g(x) and

(b) x = h(y), if they exist.

(a) To find the explicit function y = g(x), if it exists, solve the implicit function f(x, y) algebraically for y in terms of x. If for each value of x, there is one and only one value of y, the explicit function y = g(x) exists. Thus, from (4.78),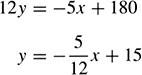

Since there is only one value of y for each value of x,

(b) To find the explicit function x = h(y), if it exists, solve the implicit function f(x, y) algebraically for x in terms of y. If for each value of y, there is one and only one value of x, the explicit function x = h(y) exists. Thus, from (4.78),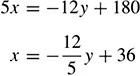

Since there is only one value of x for each value of y,

Note that when two explicit functions can be derived from the same implicit function in two variables, the explicit functions are inverse functions of each other, as shown in Problem 4.28.

f(x, y) =5x+12y-180 = 0 (4.78)