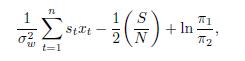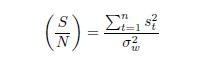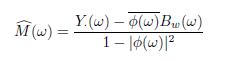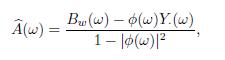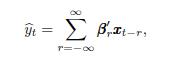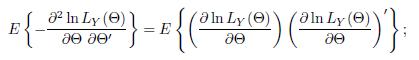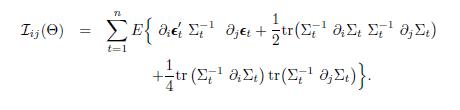Time Series Analysis And Its Applications With R Examples 2nd Edition Robert H. Shumway, David S. Stoffer - Solutions
Unlock a deeper understanding of "Time Series Analysis And Its Applications With R Examples 2nd Edition" by accessing our comprehensive solution manual. Delve into expertly crafted answers key and solutions PDF, designed for both students and instructors. Explore solved problems with step-by-step answers to enhance your learning experience. Our online platform provides questions and answers that align with the textbook, ensuring a thorough grasp of each chapter. Benefit from the test bank and instructor manual for a well-rounded comprehension. Enjoy the convenience of free download options for these invaluable resources.
![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()