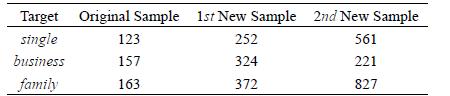
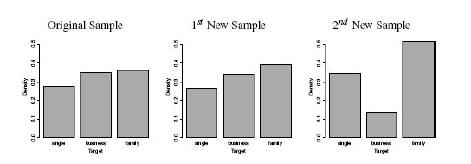
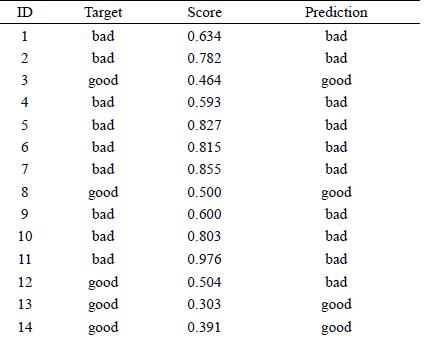
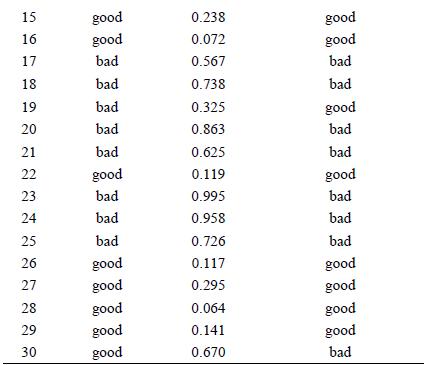
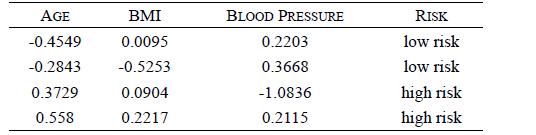
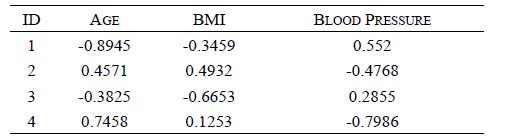
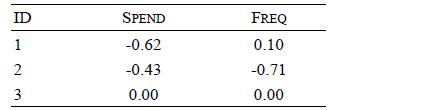
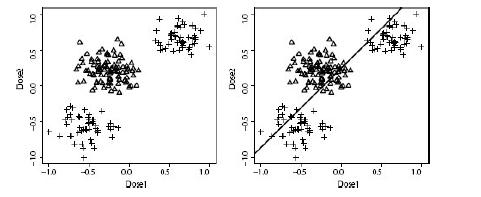
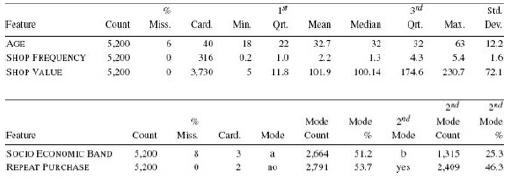
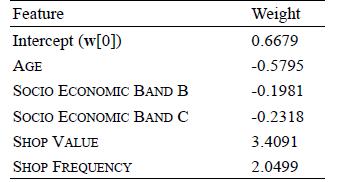
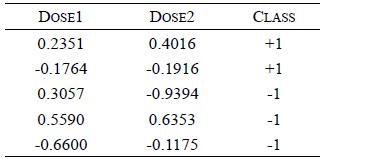
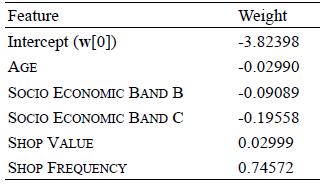
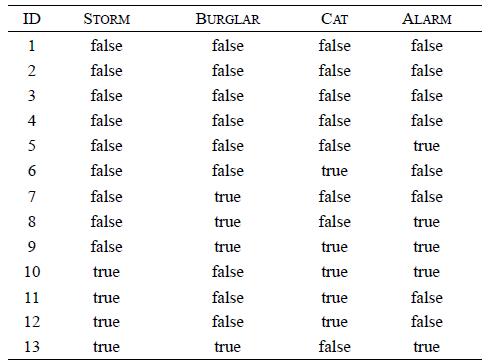
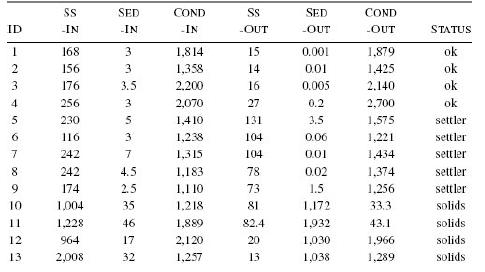
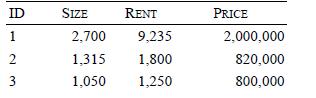
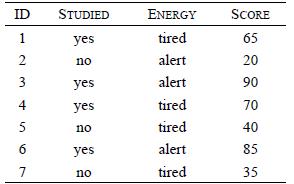
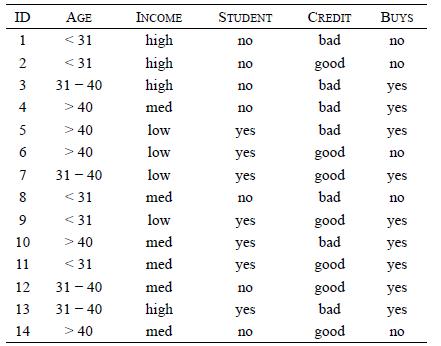
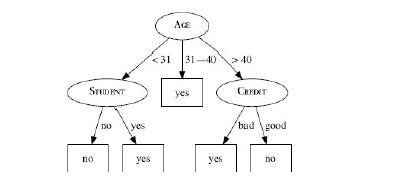
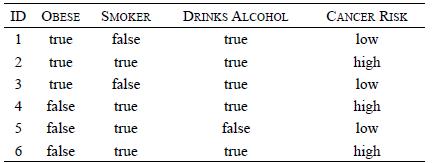
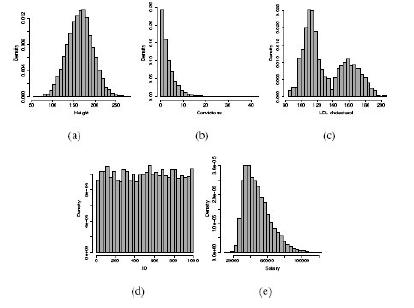
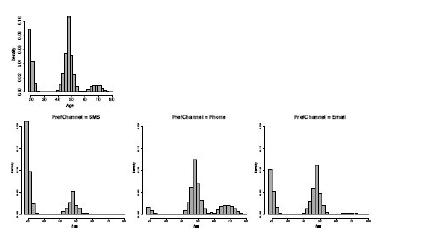
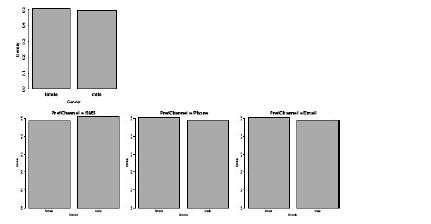
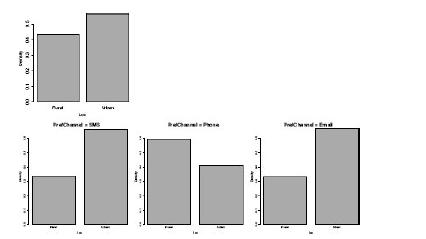
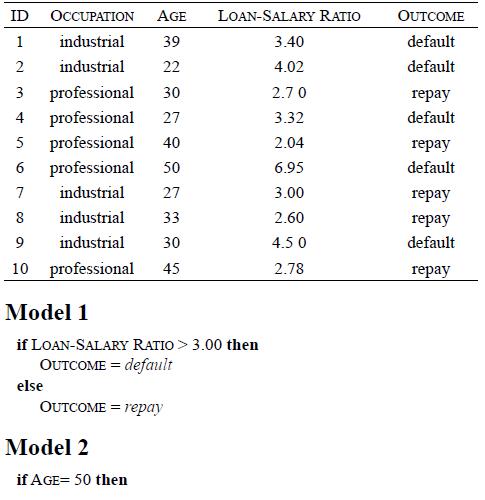
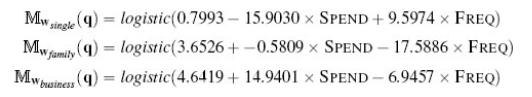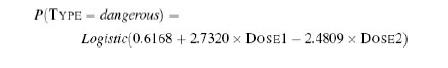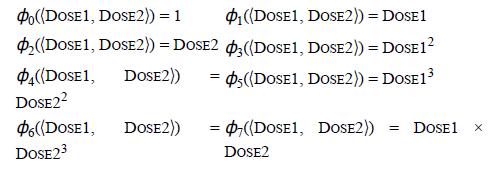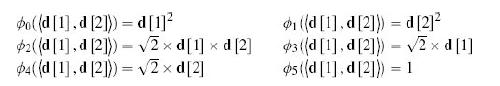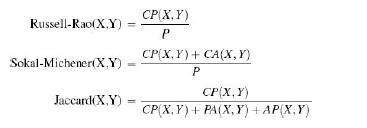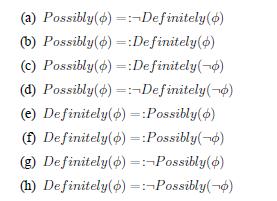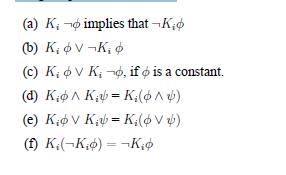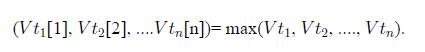Distributed Computing Principles Algorithms And Systems 1st Edition Ajay D. Kshemkalyani, Mukesh Singhal - Solutions
Discover comprehensive solutions for "Distributed Computing Principles Algorithms and Systems 1st Edition" by Ajay D. Kshemkalyani and Mukesh Singhal. Access an extensive range of online resources, including answers key and solutions pdf, to enhance your understanding of solved problems. Our solution manual provides chapter solutions and step-by-step answers tailored for every question and answer in the textbook. Whether you need a test bank or an instructor manual, find all the tools you need to excel in distributed computing. Enjoy the convenience of free download options to support your academic journey.
![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()