Identical blocks of unit length are stacked on top of each other at the edge of a table. The center of gravity of the top block must lie over the block below it, the center of gravity of the top two blocks must lie over the block below them, and so on (see figure).

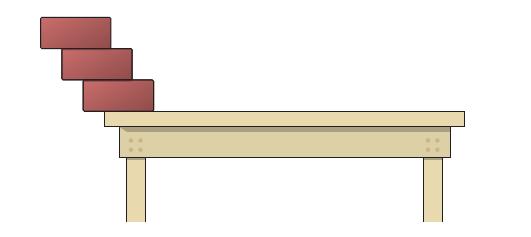
(a) When there are three blocks, show that it is possible to stack them so that the left edge of the top block extends 11/12 unit beyond the edge of the table.
(b) Is it possible to stack the blocks so that the right edge of the top block extends beyond the edge of the table?
(c) How far beyond the table can the blocks be stacked?