Consider the integral in Example 1: Show that the integrand can be expressed as a product g(x)h(y)k(z).
Question:
Consider the integral in Example 1:
![EXAMPLE 1 Integration over a Box Calculate the integral [+ afff x ex +32 dV, where B= [1,4]x [0,3] x [2,6].](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1705/4/0/2/87965a661ff456051705402881472.jpg)
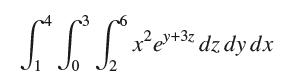
Show that the integrand can be expressed as a product g(x)h(y)k(z). Then verify the equation in Exercise 27 by computing the product of integrals on the right-hand side and showing it equals the result obtained in the example.
Data From Exercise 27
Assume ƒ(x, y, z) can be expressed as a product, ƒ(x, y, z) = g(x)h(y)k(z). Show that the integral of ƒ over a box B = [a, b] × [c, d] × [p, q] can be expressed as a product of integrals as follows:
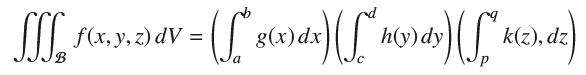
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





