Let C be a curve in R³ not passing through the origin. The cone on C is the surface consisting of all lines passing through the origin and a point on C [Figure 19(A)].

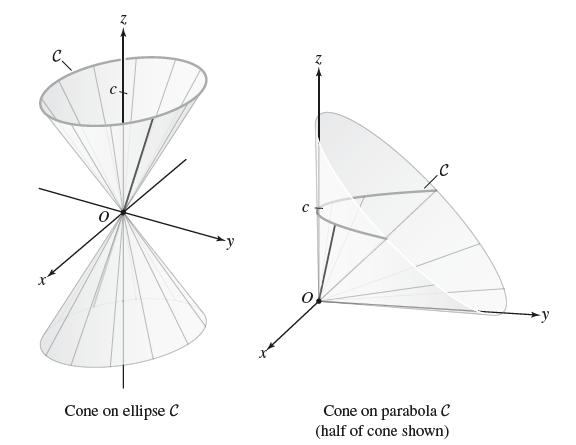
Let a and c be nonzero constants and let C be the parabola at height c consisting of all points (x, ax², c) [Figure 19(B)]. Let S be the cone consisting of all lines passing through the origin and a point on C. This exercise shows that S is also an elliptic cone.

(a) Show that S has equation yz = acx².

(b) Show that under the change of variables y = u + v and z = u − v, this equation becomes acx² = u² − v² or u² = acx² + v² (the equation of an elliptic cone in the variables x, v, u).

Transcribed Image Text:

Cone on ellipse C Cone on parabola C (half of cone shown)