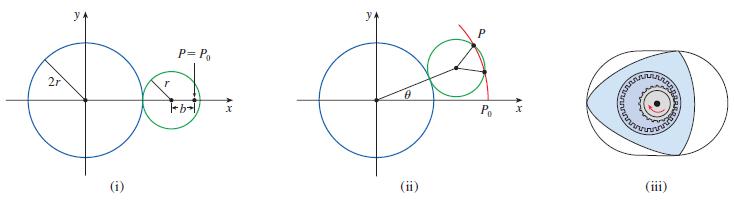
A circle C of radius 2r has its center at the origin. A circle of radius r
Question:
A circle C of radius 2r has its center at the origin. A circle of radius r rolls without slipping in the counterclockwise direction around C. A point P is located on a fixed radius of the rolling circle at a distance b from its center, 0 < b < r. Let L be the line from the center of C to the center of the rolling circle and let be the angle that L makes with the positive x-axis.
(a) Using θ as a parameter, show that parametric equations of the path traced out by P are
x = b cos 3θ + 3r cos θ y = b sin 3θ + 3r sin θ
(b) Graph the curve for various values of b between 0 and r.
(c) Show that an equilateral triangle can be inscribed in the epitrochoid and that its centroid is on the circle of radius b centered at the origin.
(d) In most rotary engines the sides of the equilateral triangles are replaced by arcs of circles centered at the opposite vertices as in part (iii) of the figure.
Step by Step Answer:
a Since the smaller circle rolls without slipping around C the amount of arc traversed on C 2r in the figure must equal the amount of arc of the smaller circle that has been in contact with C Since the smaller circle has radius r it must have turned through an angle of 2rr 2 In addition to turning through an angle 2 the little circle has rolled through an angle against C Thus P has turned through an angle of 3 as shown in the figure If the little circle had turned through an angle of 2 with its center pinned to the xaxis then P would have turned only 2 instead of 3 The movement of the little circle around C adds to the angle From the figure we see that the center of the small ...View the full answer
Calculus Early Transcendentals
ISBN: 9781337613927
9th Edition
Authors: James Stewart, Daniel K. Clegg, Saleem Watson, Lothar Redlin
