The set of all points within a perpendicular distance r from a smooth simple curve C in R³ form a “tube,” which we denote by Tube(C, r); see the figure at the left. (We assume that r is small enough that the tube does not intersect itself.) It may seem that the volume of such a tube would depend on the twists and turns of C, but in this problem you will find a formula for the volume of Tube(C, r) which, perhaps surprisingly, depends only on r and the length of C. We assume that C is parameterized with respect to arc length s as r(s), where a ≤ s ≤ b, so the arc length of C is L = b − a.

(a) Show that the surface of Tube(C, q) is parameterized by

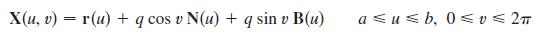
where N and B are the unit normal and binormal vectors for C.

(b) Use the Frenet-Serret Formulas and the Pythagorean Theorem for vectors to show that

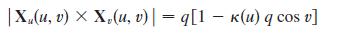
and so the surface area of Tube(C, q) is

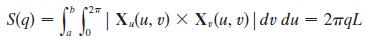
(c) Consider a thin tubular shell of radius q and thickness Δq along C, a cross-section of which is shown in the figure.

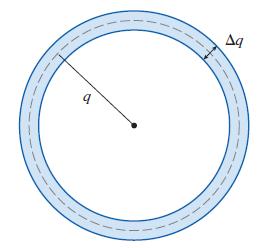
Observe that the volume of the shell is approximately Δq S(q) and conclude that the volume of Tube(C, r) is

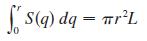
(d) Find the volume of a tube of radius r = 0.2 around the helix r(t) = (cos t, sin t, t), 0 ≤ t ≤ 4π.

(e) Find the volume of the torus.

Transcribed Image Text:

X(u, v) = r(u) + q cos v N(u) + q sin v B(u) a