The compressor discussed in Illustrations 3.4-4 and 4.5-1 is being used to compress air from 1 bar and 290 K to 10 bar. The compression can be assumed to be adiabatic, and the compressed air is found to have an outlet temperature of 575 K.

a. What is the value of ΔS for this process? 

b. How much work, W_s, is needed per mole of air for the compression? 

c. The temperature of the air leaving the compressor here is higher than in Illustration 4.5-1. How do you account for this?

In your calculations you may assume air is an ideal gas with C^∗_P = 29.3 J/(mol K).

Illustrations 3.4-4

Example of a Thermodynamics Problem that Cannot Be Solved with Only the Mass and Energy Balances

A compressor is a gas pumping device that takes in gas at low pressure and discharges it at a higher pressure. Since this process occurs quickly compared with heat transfer, it is usually assumed to be adiabatic; that is, there is no heat transfer to or from the gas during its compression. Assuming that the inlet to the compressor is air [which we will take to be an ideal gas with C^∗_P = 29.3 J/(mol K)] at 1 bar and 290 K and that the discharge is at a pressure of 10 bar, estimate the temperature of the exit gas and the rate at which work is done on the gas (i.e., the power requirement) for a gas flow of 2.5 mol/s.

Illustrations 4.5-1

Illustration 3.4-4 Continued, Using the Entropy Balance 

In Illustration 3.4-4 we tried to estimate the exit temperature and power requirements for a gas compressor. From the steady-state mass balance we found that

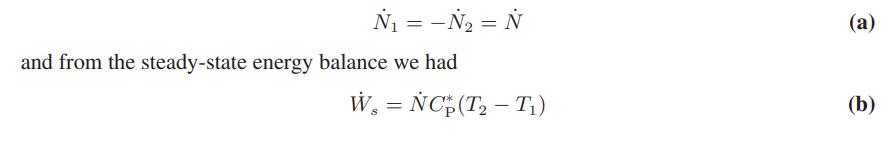
which resulted in one equation (Eq. b) with two unknowns, Ẇ_s and T₂. Now, writing a molar entropy balance for the same system yields

To obtain an estimate of the exit temperature and the power requirements, we assume that the compressor is well designed and operates reversibly, that is 

Thus T₂ is known, and hence W_s can be computed:

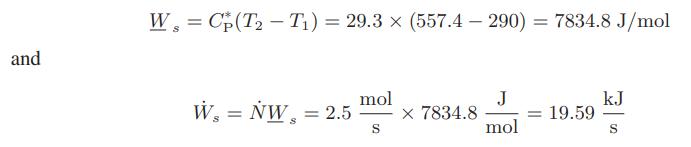
Before considering the problem to be solved, we should try to assess the validity of the assumption Ṡ_gen = 0. However, this can be done only by experiment. One method is to measure the inlet and exit temperatures and pressures for an adiabatic turbine and see if Eq. e is satisfied. Experiments of this type indicate that Eq. e is reasonably accurate, so that reversible operation is a reasonable approximation for a gas compressor.

Transcribed Image Text:

N₁ = -N₂ = N and from the steady-state energy balance we had W₂ = NCP (T₂ - T₁) (a) (b)