Consider for illustration the diffusion-reaction problem given by [begin{equation*}frac{d^{2} c}{d x^{2}}=M c^{2} tag{14.54}end{equation*}] with the same boundary
Question:
Consider for illustration the diffusion-reaction problem given by
\[\begin{equation*}\frac{d^{2} c}{d x^{2}}=M c^{2} \tag{14.54}\end{equation*}\]
with the same boundary conditions as before.
Use the expansion for \(c\) in terms of \(M\) as in Eq. (14.24) for small values of \(M\), which is a regular perturbation problem. Show that by substituting into the differential equation we obtain
\[\begin{equation*}M f_{1}^{\prime \prime}+M^{2} f_{2}^{\prime \prime}+\cdots=M+2 M^{2} f_{1}+O\left(M^{3}\right) \tag{14.55}\end{equation*}\]
By equating the powers of \(M\), write out the governing equations for \(f_{1}\) and \(f_{2}\). Integrate the equations to obtain the following results:
\[f_{1}=x^{2}-x\]
and
\[f_{2}=\left(x^{4} / 4-x^{3}+2 x\right) / 3\]
Derive an expression for the effectiveness factor, and show that it can be approximated as \(1-2 M / 3\) to an approximation of \(O\left(M^{2}\right)\). Derive the next approximation.
Also solve the problem numerically using BVP4C and compare the results.
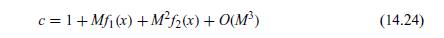
Step by Step Answer:

Advanced Transport Phenomena Analysis Modeling And Computations
ISBN: 9780521762618
1st Edition
Authors: P. A. Ramachandran





