Repeat Problem 10.D9, calculating the diameter at the top, but condense the feed to a saturated liquid. Determine \((\mathrm{L} / \mathrm{D})_{\min }\) and \(\mathrm{L} / \mathrm{D}=\) \(1.43 \times(\mathrm{L} / \mathrm{D})_{\text {min }}\). Compare the diameter of this column to the diameter of \(10.27 \mathrm{ft}\) calculated for Problem 10.D9. Calculate the ratio \(Q_{R, \text { liquid_feed }} / Q_{R, \text { vapor_feed }}\) for this problem.

Problem 10.D9

Table 2-3

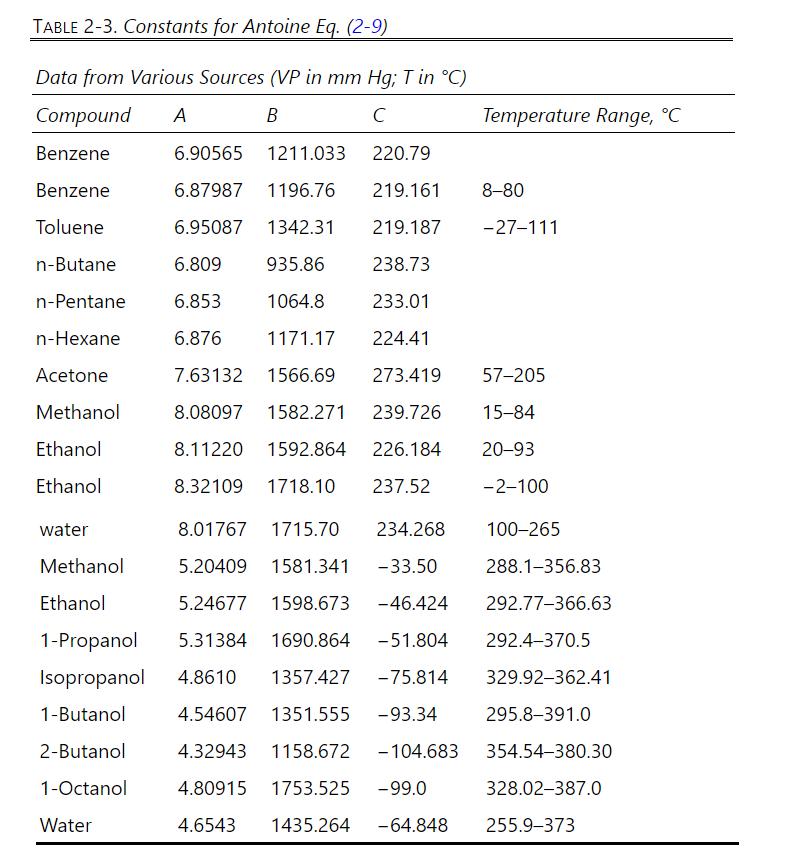
Table 2-8

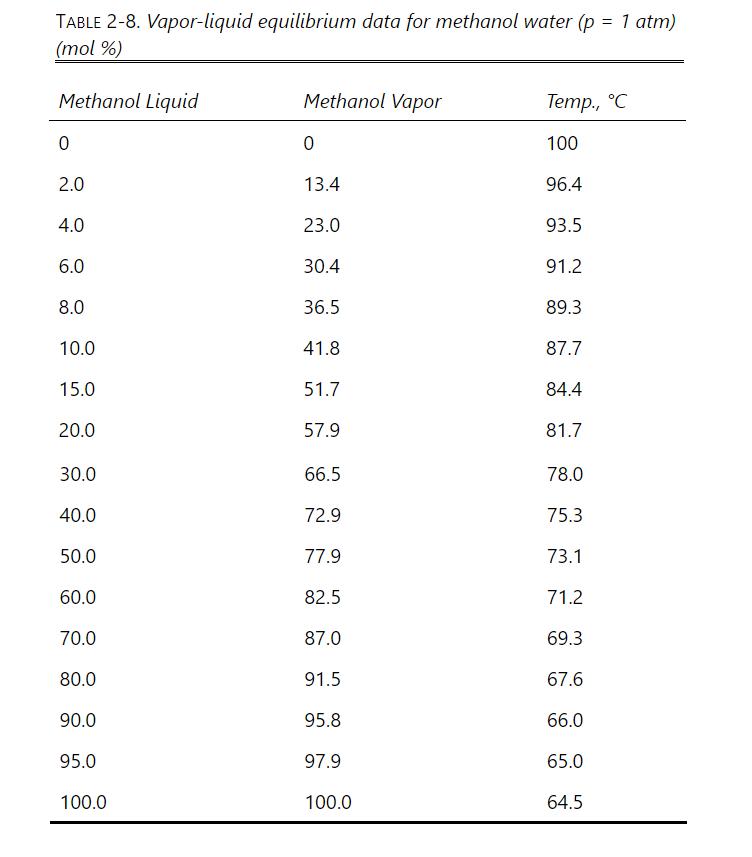
D9.* 1000.0 kmol/h of a saturated vapor feed that is 60.0 mol% methanol and 40.0 mol% water is distilled in a sieve plate column operating at 75% of flooding velocity. Distillate is 99.9 mol% methanol, and bottoms is 1.0 mol% methanol. L/V = 0.6 and p = 1.0 atm. Use a 0.4572-m tray spacing and n = 0.90. Density of pure liquid methanol is 0.7914 g/ml. Data are available in Table 2-8 and Table 2-3. Assume an ideal gas. The surface tension of pure methanol can be estimated as = 24.0 - 0.0773 T with T in C (Dean, 1985, p. 10-110). . Calculate the diameter based on the conditions at the top of the column. Calculate (L/D) min and multiplier M = (L/D)/(L/D)min-