1.

Revisit the data in Table 2-1 Raw Data and calculate the batch reactor (BR) times to achieve 10%, 50%, and 80% conversion when 100 moles of A are charged to a 400 dm3 reactor.

Table 2-1

2.

Revisit Examples 2-1 through 2-3. How would your answers change if the flow rate, FA0, were cut in half? If it were doubled? What conversion can be achieved in a 4.5 m3 PFR and in a 4.5 m3 CSTR?

Examples 2-1

The reaction described by the data in Table 2-2 A → B is to be carried out in a CSTR.

Table 2-2

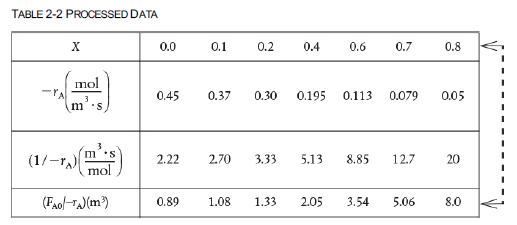
Species A enters the reactor at a molar flow rate of FA0=0.4mo1s, which is the flow rate used to construct the Levenspiel plot in Figure 2-2(b).

Figure 2-2(b)

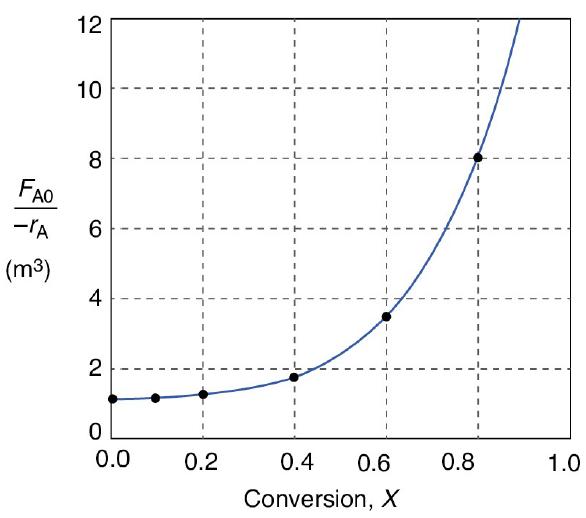1. Using the data in either Table 2-2 or Figure 2-2(b), calculate the volume necessary to achieve 80% conversion in a CSTR.
2. Shade the area in Figure 2-2(b) that would give the CSTR volume necessary to achieve 80% conversion.

Examples 2-2

The reaction described by the data in Tables 2-1 and 2-2 is to be carried out in a PFR. The entering molar flow rate of A is again, FA0 = 0.4 mol/s.
1. First, use one of the integration formulas to determine the PFR reactor volume necessary to achieve 80% conversion.
2. Next, shade the area in Figure 2-2(b) that would give the PFR volume necessary to achieve 80% conversion.
3. Finally, make a qualitative sketch of the conversion, X, and the rate of reaction, –rA, down the length (volume) of the reactor.

Tables 2-1

Examples 2-3

Compare the volumes of a CSTR and a PFR required for the same conversion using the data in Figure 2-2(b). Which reactor would require the smaller volume to achieve a conversion of 80%: a CSTR or a PFR? The entering molar flow rate and the feed conditions are the same in both cases.

Figure 2-2(b)

3.

Revisit Example 2-2. Being a company about to go bankrupt, you can only afford a 2.5 m3 CSTR. What conversion can you achieve?

The reaction described by the data in Tables 2-1 and 2-2 is to be carried out in a PFR. The entering molar flow rate of A is again, FA0 = 0.4 mol/s.
1. First, use one of the integration formulas to determine the PFR reactor volume necessary to achieve 80% conversion.
2. Next, shade the area in Figure 2-2(b) that would give the PFR volume necessary to achieve 80% conversion.
3. Finally, make a qualitative sketch of the conversion, X, and the rate of reaction, –rA, down the length (volume) of the reactor.

Tables 2-1

4.

Revisit Example 2-3. What conversion could you achieve if you could convince your boss, Dr. Pennypincher, to spend more money to buy a 1.0 m³ PFR to attach to a 2.40 CSTR?

Figure 2-2(b)

5.

Revisit Example 2-4. How would your answers change if the two CSTRs (one 0.82 m3 and the other 3.2 m³) were placed in parallel with the flow, FA0, divided equally between the reactors?

Example 2-4

For the two CSTRs in series, 40% conversion is achieved in the first reactor. What is the volume of each of the two reactors necessary to achieve 80% overall conversion of the entering species A?

6.

Revisit Example 2-5.

(1) What is the worst possible way to arrange the two CSTRs and one PFR?

(2) What would be the reactor volumes if the two intermediate conversions were changed to 20% and 50%, respectively?

(3) What would be the conversions, X₁, X₂, and X₃, if all the reactors had the same volume of 100 dm³ and were placed in the same order?

Example 2-5

The isomerization of butane

7.

Revisit Example 2-6. If the term CA0∫0XdX-rA is 2 seconds for 80% conversion, how much fluid (m³/min) can you process in a 3 m³ reactor?

Example 2-6

Calculate the space time, τ, and space velocities for the reactor in Examples 2-1 and 2-3 for an entering volumetric flow rate of 2 dm³/s.

Examples 2-1

The reaction described by the data in Table 2-2 A → B is to be carried out in a CSTR.

Table 2-2

Example 2-3

Compare the volumes of a CSTR and a PFR required for the same conversion using the data in Figure 2-2(b). Which reactor would require the smaller volume to achieve a conversion of 80%: a CSTR or a PFR? The entering molar flow rate and the feed conditions are the same in both cases.

Figure 2-2(b)

Transcribed Image Text:

X -TA (mol/m. s) 0 0.45 0.1 0.37 0.2 0.4 0.6 0.30 0.195 0.113 0.7 0.079 0.8 0.05