a. Example 14-1: Mass Transfer of Oxygen to a Burning Carbon Particle Wolfram and Python 1. Vary
Question:
a. Example 14-1: Mass Transfer of Oxygen to a Burning Carbon Particle Wolfram and Python
1. Vary each slider to find the parameter to which the flux WAr is most sensitive.
2. What happens when the liquid diffusity and viscosity are both increased simultaneously?
3. Vary the velocity as shown in Figure 14-5 and describe its effect on the flux.
4. Write a set of conclusions based on the above experiments.
Figure 14-5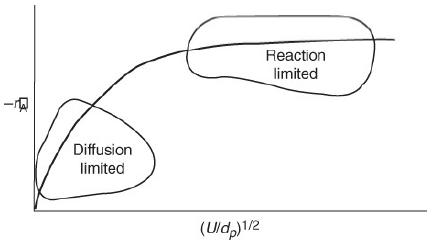
Example 14-1
A schematic of the transfer of oxygen to the particle is shown in Figure 14-4. The gas-phase diffusivity in the flame (1000 K) surrounding the particle is taken as 10–4 m2/s and the particle diameter is 50 μm (5 × 10–5 m). The concentration of oxygen in the bulk air (21% at 1 atm and 298 K) is 8.58 mol/m3. The reaction is virtually instantaneous so that the concentration of oxygen on the surface of the particle is zero, that is, CAs = 0. The heat of reaction is ΔHRx = –93.5 kJ/mol carbon. Calculate molar flux, WA (mol/m2/s) and molar flow m˙A (mol/s) to the particle. For a dust cloud density of 200 g/m3, calculate the heat generated per particle q˙p, and the heat generated per volume of cloud.
Figure 14-4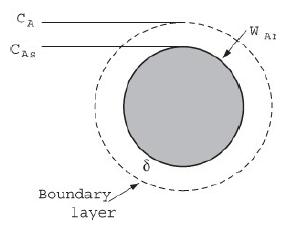
b. Example 14-2: Rapid Liquid-Phase Reaction on the Surface of a Catalyst Wolfram and Python
1. Vary each of the parameters and tell which one the mass transfer coefficient (kc) is most sensitive.
2. Change DAB and U simultaneously both up and down and describe what you find.
3. Write a set of three conclusions from your experiments (i) and (ii).
Example 14-2
Calculate the molar flux, WAr, of reactant A to a single catalyst pellet 1 cm in diameter suspended in a large body of liquid B. The reactant is present in dilute concentrations, and the reaction is considered to take place instantaneously at the external pellet surface (i.e., CAs ≃ 0). The bulk concentration of the reactant A is 1.0 M, and the free-stream liquid velocity past the sphere is 0.1 m/s. The kinematic viscosity (i.e., μρ) is 0.5 centistoke (cS; 1 centistoke = 10-6 m2/s), and the liquid diffusivity o A in B is DAB = 10–10 m2/s at 300 K.
c. Example 14-3: Combustion Time for a Single Particle
Wolfram and Python
1. Compare the burning time for a 100 μm porous carbon particle with a 10% solid with tc in Example 14-3.
2. Vary all the parameters you can think of that would give a burning time of 500 ms.
3. Write a set of conclusions from your Wolfram experiments (i) and (ii).
Example 14-3
There is a 100 micron carbon dust particle in air at 1 atm. Calculate KS and the time for the particle to burn completely (dp = 0). The average value of the diffusivity near the burning particle is 10–4 m2/s and the density of the carbon particle is 2.26 × 106 g/m3.
d. Example 14-4: Mass Transfer Effects in Maneuvering a Space Satellite. What if you were asked for representative values for Re, Sc, Sh, and kc for both liquid- and gas-phase systems for a velocity of 10 cm/s and a pipe diameter of 5 cm (or a packed-bed diameter of 0.2 cm)? What numbers would you give?
Example 14-4
Hydrazine has been studied extensively for use in monopropellant thrusters for space flights of long duration. Thrusters are used for altitude control of communication satellites. Here, the decomposition of hydrazine over a packed bed of alumina-supported iridium catalyst is of interest. In a proposed study, a 2% hydrazine in 98% helium mixture is to be passed over a packed bed of cylindrical particles 0.25 cm in diameter and 0.5 cm in length at a gas-phase velocity of 150 m/s and a temperature of 450 K. The kinematic viscosity of helium at this temperature is 4.94 × 10–5 m2/s. The hydrazine decomposition reaction is believed to be externally mass transfer-limited under these conditions. If the packed bed is 0.05 m in length, what conversion can be expected? Assume isothermal operation. O. I. Smith and W. C. Solomon, Ind. Eng. Chem. Fund., 21, 374. Actual case history and current application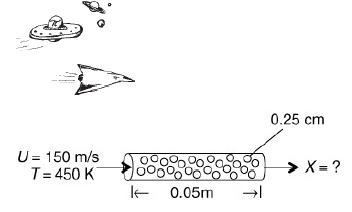
The packet-bed reactor (PBR) is a horizontal cylindrical tube with the cylindrical particles of diameter 0.25 centimeters and the length of the PBR is 0.05 meters. On the left, the gas-phase velocity (U) enters the PBR at the speed of 150 meters per second at a temperature of 450 Kelvin. On the right end of the PBR tube, the expected conversion (X) is marked as an unknown value.
Additional information: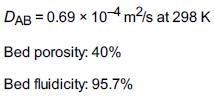
e. Example 14-5: The Case of Divide and Be Conquered. How would your answers change if the reaction were carried out in the liquid phase where kinematic viscosity, υ, varied as v(T2)=v(T1)exp[−400 K(1T1−1T2)]?
Example 14-5
A mass transfer-limited reaction is being carried out in two reactors of equal volume and packing, connected in series as shown in Figure E14-5.1. Currently, 86.5% conversion is being achieved with this arrangement. It is suggested that the reactors be separated and the flow rate be divided equally among each of the two reactors (Figure E14-5.2) to decrease the pressure drop and hence the pumping requirements. In terms of achieving a higher conversion, Robert is wondering if this is a good idea.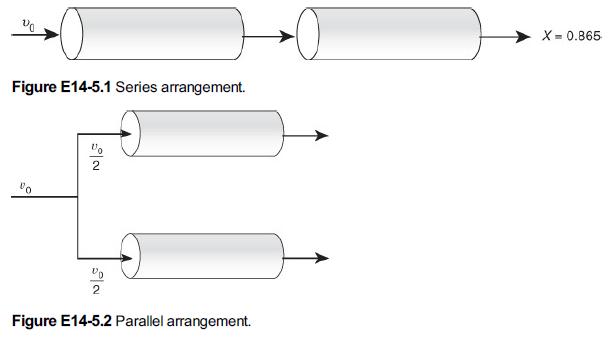
Step by Step Answer:






