Using the bending formulae (6.6.9), compare the maximum bending stresses from the cases presented in Example 6.2 and Exercise 6.18 . Numerically compare these results with the exact solution; see (6.7.9) at midspan x = l/2.

Data from example 6.2

Consider a simply supported Euler-Bernoulli beam of length l carrying a uniform loading q_o. This one-dimensional problem has displacement boundary conditions:

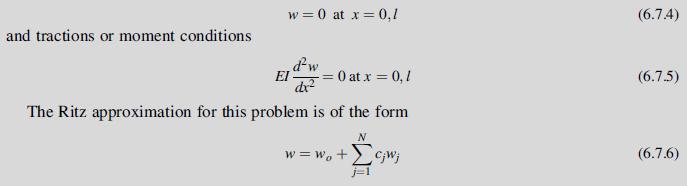
With no nonhomogeneous boundary conditions, w_o = 0. For this example, we choose a polynomial form for the trial solution. An appropriate choice that satisfies the homogeneous conditions (6.7.4) is w_j = x ^j (l – x). Note this form does not satisfy the traction conditions (6.7.5). Using the previously developed relation for the potential energy (6.6.12), we get:

Equation 6.7 .4

Equation 6.7 .5

Actually, for this special case, the exact solution can be obtained from a Ritz scheme by including polynomials of degree three.

Equation 6.6 .9

Equation 6.7 .9

Data from exercise 6.18

Rework Example 6.2 using the trigonometric Ritz approximation w_j = sin jπx/l. Develop a two-term approximate solution and compare it with the displacement solution developed in the text. Also compare each of these approximations with the exact solution (6.7.9) at midspan x = l/2.

Transcribed Image Text:

and tractions or moment conditions w = 0 at x = 0,1 dw dx The Ritz approximation for this problem is of the form w = wo+Cjw; = = 0 at x = 0, / (6.7.4) (6.7.5) (6.7.6)