One of the most surprising probability distributions found in practice is given by a rule known as
Question:
One of the most surprising probability distributions found in practice is given by a rule known as Benford’s law. This probability distribution concerns the first digits of numbers. The first digit of a number may be any of the digits 1, 2, 3, 4, 5, 6, 7, 8, or 9. It is reasonable to believe that, for most sets of numbers encountered in practice, these digits would occur equally often.
In fact, it has been observed that for many naturally occurring data sets, smaller numbers occur more frequently as the first digit than larger numbers do. Benford’s law is named for Frank Benford, an engineer at General Electric, who stated it in 1938.
Following are the populations of the 50 states in July 2015, as estimated by the U.S. Census Bureau. The first digit of each population number is listed separately.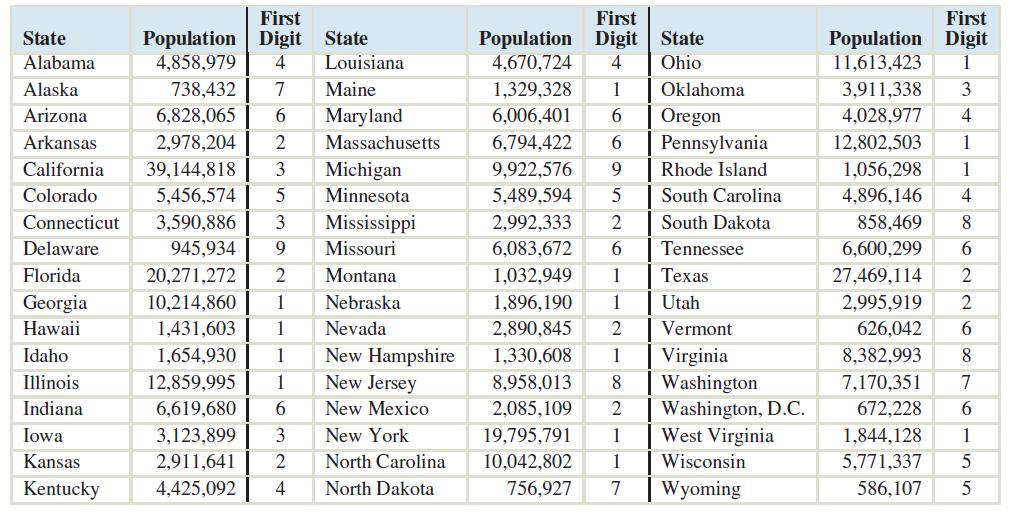
Here is a frequency distribution of the first digits of the state populations: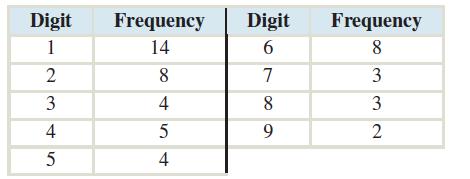
For the state populations, the most frequent first digit is 1, with 7, 8, and 9 being the least frequent.
Now here is a table of the closing value of the Dow Jones Industrial Average for each of the years 1975–2016.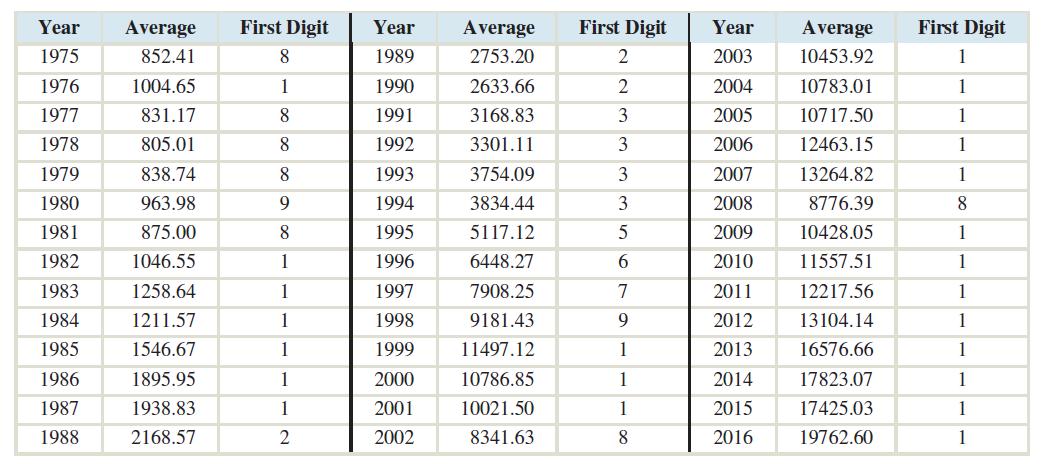
Here is a frequency distribution of the first digits of the stock market averages: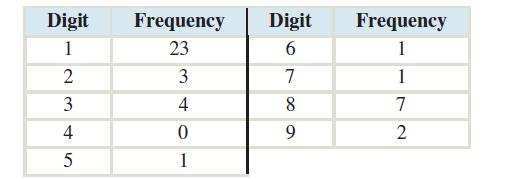
For the stock market averages, the most frequent first digit by far is 1.
The stock market averages give a partial justification for Benford’s law. Assume the stock market starts at 1000 and goes up 10% each year. It will take 8 years for the average to exceed 2000. Thus, the first eight averages will begin with the digit 1.
Now imagine that the average starts at 5000. If it goes up 10% each year, it would take only 2 years to exceed 6000, so there would be only 2 years starting with the digit 5. In general, Benford’s law applies well to data where increments occur as a result of multiplication rather than addition, and where there is a wide range of values. It does not apply to data sets where the range of values is small.
Here is the probability distribution of digits as predicted by Benford’s law: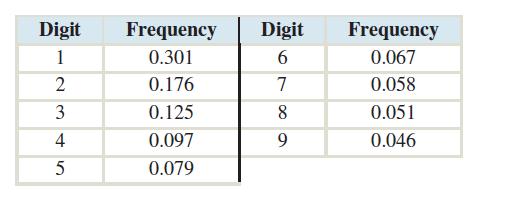
The surprising nature of Benford’s law makes it a useful tool to detect fraud. When people make up numbers, they tend to make the first digits approximately uniformly distributed; in other words, they have approximately equal numbers of 1s, 2s, and so on. Many tax agencies, including the Internal Revenue Service, use software to detect deviations from Benford’s law in tax returns.
Following are results from three hypothetical corporate tax returns. Each purports to be a list of expenditures, in dollars, that the corporation is claiming as deductions. Two of the three are genuine, and one is a fraud. Which one is the fraud?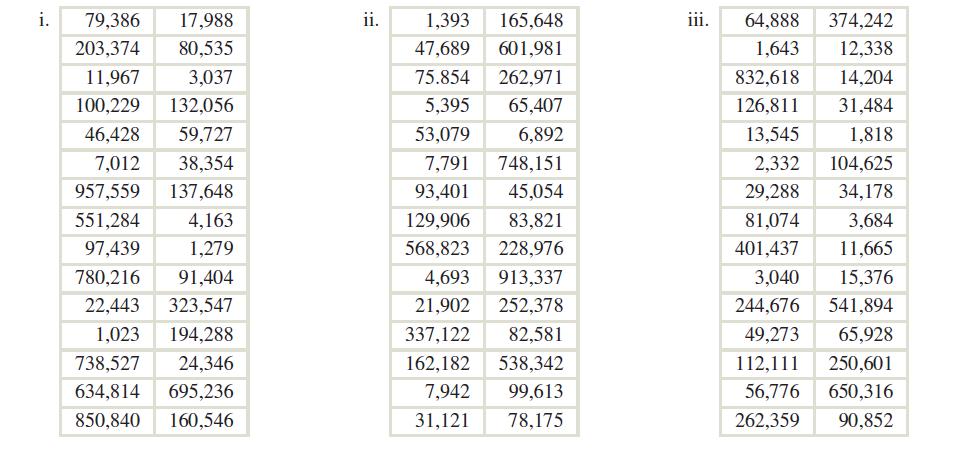
Step by Step Answer:






