Consider a floating cylindrical buoy with radius r, height h, and uniform density 0.5 (recall

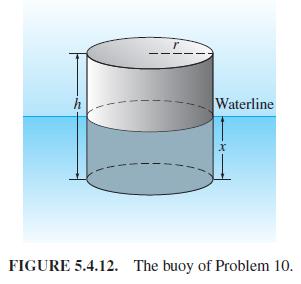
Consider a floating cylindrical buoy with radius r, height h, and uniform density ρ ≦ 0.5 (recall that the density of water is 1 g/cm³). The buoy is initially suspended at rest with its bottom at the top surface of the water and is released at time t = 0. Thereafter it is acted on by two forces: a downward gravitational force equal to its weight mg = ρπr²hg and (by Archimedes' principle of buoyancy) an upward force equal to the weight πr²xg of water displaced, where x = x (t) is the depth of the bot- tom of the buoy beneath the surface at time t (Fig. 5.4.12). Assume that friction is negligible. Conclude that the buoy undergoes simple harmonic motion around its equilibrium position x_e = ρh with period p = 2π√ρh/g. Compute p and the amplitude of the motion if ρ = 0.5 g/cm³, h = 200 cm, and g = 980 cm/s².

Transcribed Image Text:

h Waterline FIGURE 5.4.12. The buoy of Problem 10.