Consider flow through a two-dimensional slipperpad bearing with linearly decreasing gap height from h 0 to h
Question:
Consider flow through a two-dimensional slipperpad bearing with linearly decreasing gap height from h0 to hL (Fig. P10–23), namely, h = h0 + αx, where a is the nondimensional convergence of the gap, α = (hL – h0)/L. We note that tan α ≅ α for very small values of α. Thus, α is approximately the angle of convergence of the upper plate in Fig. P10–23 (α is negative for this case). Assume that the oil is exposed to atmospheric pressure at both ends of the slipper-pad, so that P = P0 = Patm at x = 0 and P = PL = Patm at x = L. Integrate the Reynolds equation for this slipper-pad bearing to generate an expression for P as a function of x.
FIGURE P10–23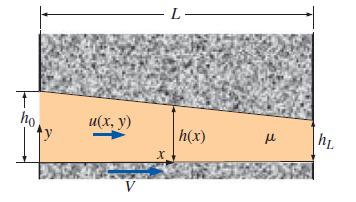
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Fluid Mechanics Fundamentals And Applications
ISBN: 9780073380322
3rd Edition
Authors: Yunus Cengel, John Cimbala
Question Posted:





