Calculate (x, 0) for a one-dimensional wave packet, when the amplitude function A(k) is given by and

Calculate ψ(x, 0) for a one-dimensional wave packet, when the amplitude function A(k) is given by

and when it is given by

For both cases, verify the validity of the uncertainty principle for wave packets, stated in the previous problem.

Data from Problem 12

Consider a one-dimensional wave packet at the instant t = 0, whose amplitude function A(k) is given by the Gaussian function

where a and k₀ are constants.

Show that ψ(x, 0) is also a Gaussian function given by

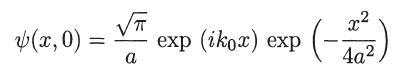
Make a plot of both A(k) and R{ψ(x, 0)}, considering that k₀ ≫ (1/a).

The average extension of the wave packet Δ̅x can be defined in terms of the root mean square deviation,

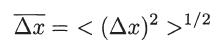
where the dispersion is given by

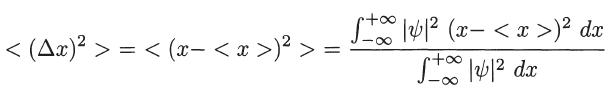
Similarly, we have

where the dispersion in k is

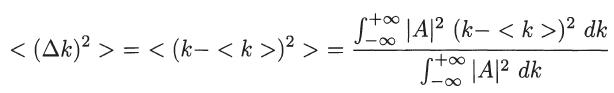
Show that for this Gaussian wave packet we have

Consequently, in this case,

It can be shown that the Gaussian wave packet is the minimum uncertainty packet and that, in general, we have the uncertainty principle

Transcribed Image Text:

A(k) = exp (-ikxo)