In the previous problem, consider that n = constant and that f₀ is the following modified Maxwell-Boltzmann distribution function:

Calculate the electron distribution function f(r, v) and show that the heat flux vector is given by

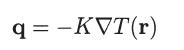
Determine the expression for the thermal conductivity K.

Data from Problem 12.

Consider problem 11.10, but taking E = 0 and, instead of the adiabatic case, consider a constant kinetic pressure

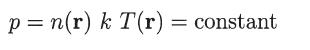
Show that the electron distribution function is given by

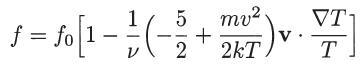
Evaluate the heat flux vector q and show that it can be written as

where the thermal conductivity K is equal to 5kp/(2mv).

What is the value of the electric current density J in this case?

Data from Problem 11.10.

An electron gas (Lorentz gas), in a background of stationary ions, is acted upon by a weak, externally applied electric field E, under steady state conditions. Using the Boltzmann equation for the electrons, with the relaxation model for the collision term (considering a constant collision frequency ν),

and considering the adiabatic case for which

show that the electron distribution function is given by

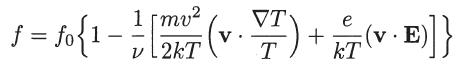
Assume that f = f₀ + f₁, where |f₁| ≪ f₀ and where f₀ is the following modified Maxwellian distribution

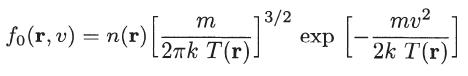
and neglect all second-order terms in the Boltzmann equation. Consider the term involving ∇f₁ as a second-order quantity.

Transcribed Image Text:

fo(r, v) = n = n [27 m [2nk T(r)] 3/2 exp mv² 2k T(r).