In a Couette viscometer the liquid to be studied fills the annular space between two cylinders, as shown in Fig. P7.1. The inner and outer radii are κR and R, respectively. The viscosity is determined by measuring the torque required to keep the inner cylinder stationary when the outer one is rotated at a constant angular velocity ω. The cylinders are long enough that the end effects associated with the top and bottom can be neglected and it can be assumed that v and ℘ are independent of z as well as of θ.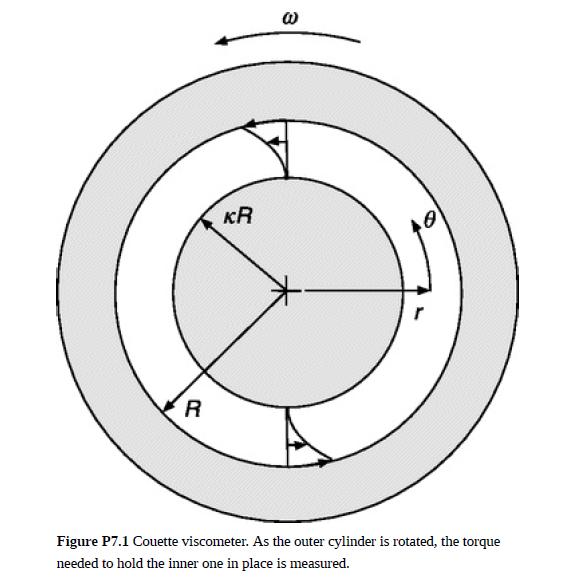

(a) Show that a unidirectional velocity field with v_θ = v_θ(r) is consistent with continuity and determine v_θ(r).

(b) Relate the torque on the inner cylinder to ω, the dimensions, and μ.

(c) As the gap between cylinders is made smaller, the shear stress at the inner one approaches that for plane Couette flow. For the torque obtained from the planar result to be within 1% of the exact value, how large must κ be?

For more on the construction and operation of Couette viscometers and a summary of findings concerning the stability of laminar flow between rotating coaxial cylinders, see Bird et al. (2002, pp. 89–93).

Transcribed Image Text:

R KR W 0 r Figure P7.1 Couette viscometer. As the outer cylinder is rotated, the torque needed to hold the inner one in place is measured.