Suppose that temperature variations within the parallel-plate channel of Fig. 7.1 noticeably alter the viscosity. In particular,
Question:
Suppose that temperature variations within the parallel-plate channel of Fig. 7.1 noticeably alter the viscosity. In particular, assume that
where α > 0. That is, there is a linear temperature variation across the channel, with T = T0 at the center and T = T1 at the upper wall. The viscosity at T = T0 is μ0 and, as is typical for liquids, μ decreases with increasing T.
(a) Determine vx(y). It is convenient to work with a dimensionless coordinate η = y/H and a dimensionless viscosity-temperature parameter A = α(T1 − T0).
(b) How does the mean velocity U compare with its value for μ = μ0?
(c) The viscosity of water (in Pa · s) is 1.139 × 10–3 at 15 °C, 1.002 × 10–3 at 20 °C, and 0.8904 × 10–3 at 25 °C. What value of α best fits these data? If the wall temperatures span this range, how much would U for water differ from that for an isothermal channel at 20 °C?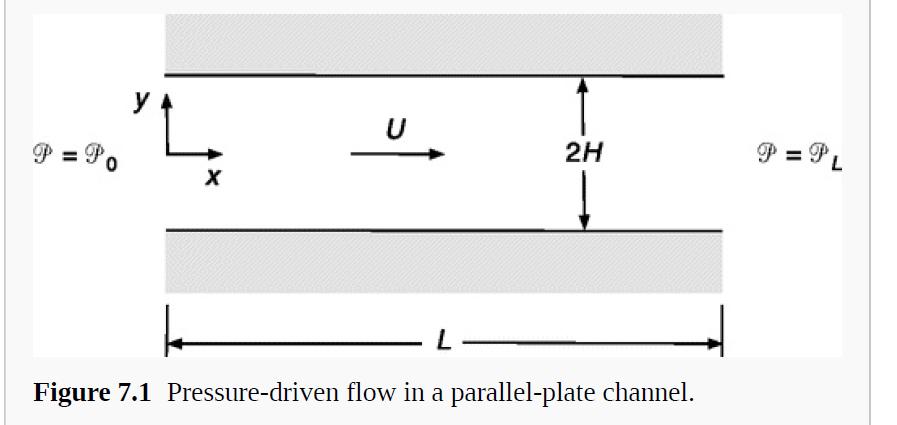
Step by Step Answer:

Introduction To Chemical Engineering Fluid Mechanics
ISBN: 9781107123779
1st Edition
Authors: William M. Deen





