Water clocks were used in Egypt and other parts of the ancient world to monitor the daily passage of time. In the version shown in Fig. P11.2 an open container of varying radius R(z) drains through a small opening of diameter d_o in its bottom. The mean velocity at the opening is v_o(t) and the water level is H(t). If the dimensions are just right, dH/dt will be constant. With each hour yielding the same decrease in H, a linear scale can be used to tell the time. You are asked to design such a clock.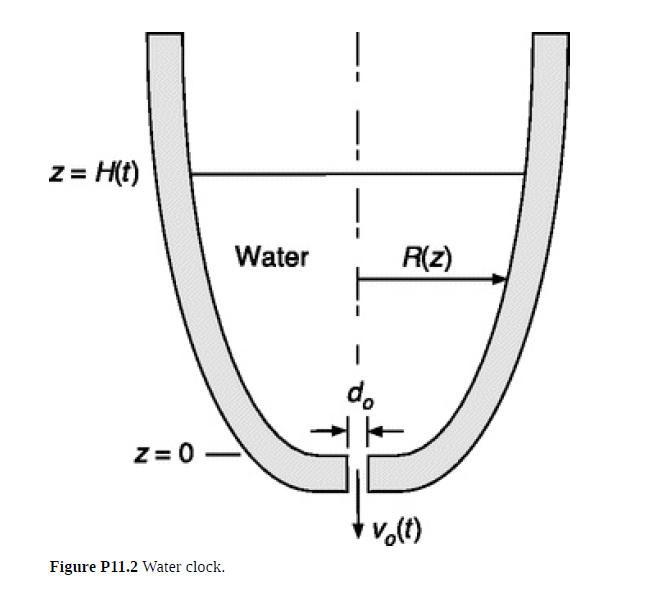

(a) Use conservation of mass to relate dH⁄dt to v_o, d_o, and R(H).

(b) Assume that vo follows Torricelli's law [Eq. (P11.1-1)] and let C = |dH/dt| be the rate of change in the water level. Identify the function R(z) that will make C constant.

(c) Express the initial water volume V₀ as a function of d_o, C, and the initial height H₀.

(d) As will be apparent in part (e), the clock should not be allowed to drain completely. Let H_f be the water level after operation for a time t_f. For a 12- hour clock that would fit in a room, choose reasonable values for H₀ – H_f and thus C.

(e) For Torricelli's law to apply, at all times the flow must be turbulent and surface tension must be negligible. To complete your design, choose values of H_f and d_o that meet those requirements. Are the resulting values of V₀, R_max[= R(H₀)], and R_min[= R(H_f)] reasonable? If not, revise your choices for the water heights and outlet diameter.

Transcribed Image Text:

z = H(t) Z=0- Figure P11.2 Water clock. Water do R(z) vo(t)