Write a program that takes a command-line argument n and creates an n-by-n boolean matrix with the element in row i and column j set to true if i and j are relatively prime, then shows the matrix on the standard drawing (see EXERCISE 1.4.16). Then, write a similar program to draw the Hadamard matrix of order n (see EXERCISE 1.4.29). Finally, write a program to draw the boolean matrix such that the element in row n and column j is set to true if the coefficient of x j in (1 + x)i (binomial coefficient) is odd (see EXERCISE 1.4.41). You may be surprised at the pattern formed by the third example.

EXERCISE 1.4.16

Write a program that takes an integer command-line argument n and creates an n-by-n boolean array a[][] such that a[i][j] is true if i and j are relatively prime (have no common factors), and false otherwise. Use your solution to EXERCISE 1.4.6 to print the array.

EXERCISE 1.4.29

The n-by-n Hadamard matrix H(n) is a boolean matrix with the remarkable property that any two rows differ in exactly n / 2 values. (This property makes it useful for designing error-correcting codes.) H(1) is a 1-by-1 matrix with the single element true, and for n > 1, H(2n) is obtained by aligning four copies of H(n) in a large square, and then inverting all of the values in the lower right n-by-n copy, as shown in the following examples (with T representing true and F representing false, as usual).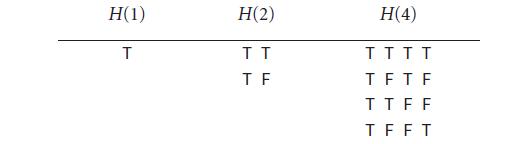

Write a program that takes an integer command-line argument n and prints H(n).
Assume that n is a power of 2.

EXERCISE 1.4.41

Write a program that takes an integer commandline argument n and creates a two-dimensional ragged array a[][] such that a[n]
[k] contains the probability that you get exactly k heads when you toss a fair coin n times. These numbers are known as the binomial distribution: if you multiply each element in row i by 2 n, you get the binomial coefficients—the coefficients of x k in (x+1)n—arranged in Pascal’s triangle. To compute them, start with a[n][0] = 0.0 for all n and a[1][1] = 1.0, then compute values in successive rows, left to right, with a[n][k] = (a[n-1][k] + a[n-1][k-1]) / 2.0.

Transcribed Image Text:

H(1) H(2) H(4) T T T TF TTTT TFT F TTF F TFF T